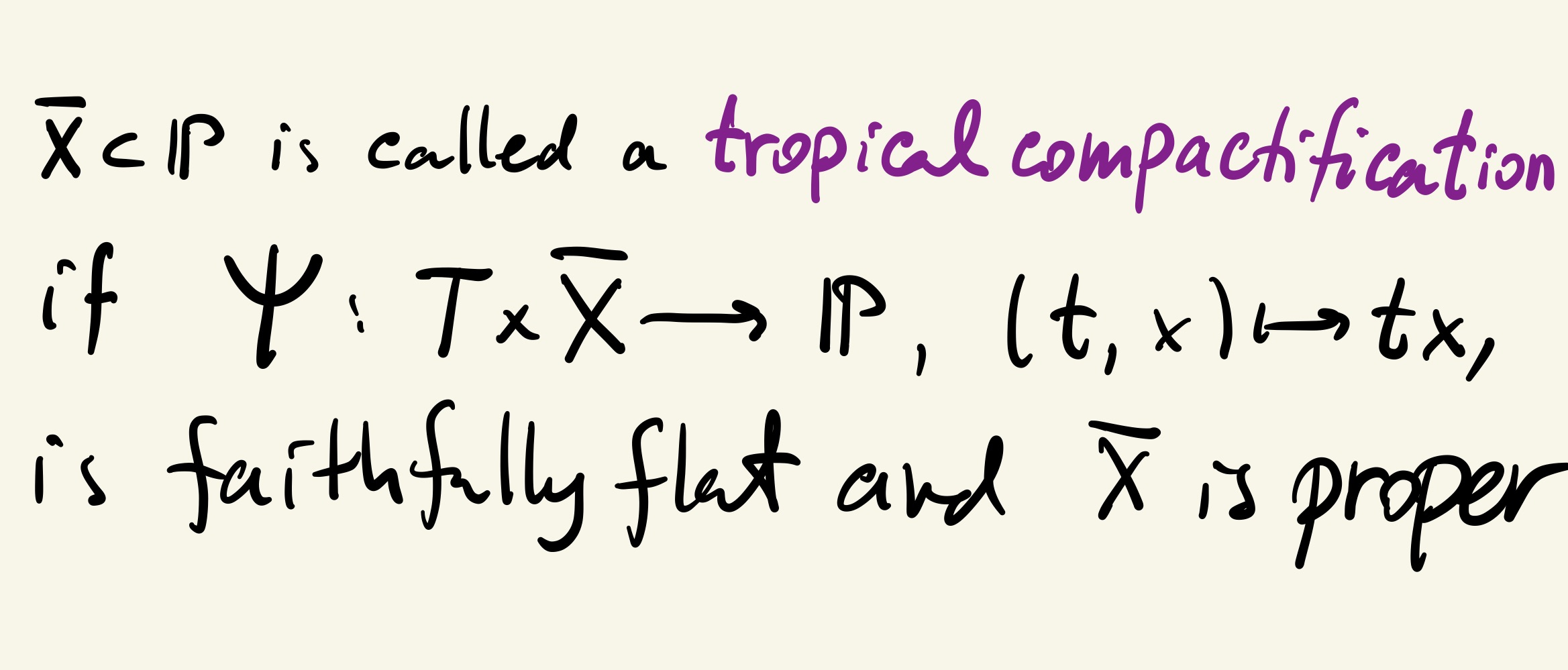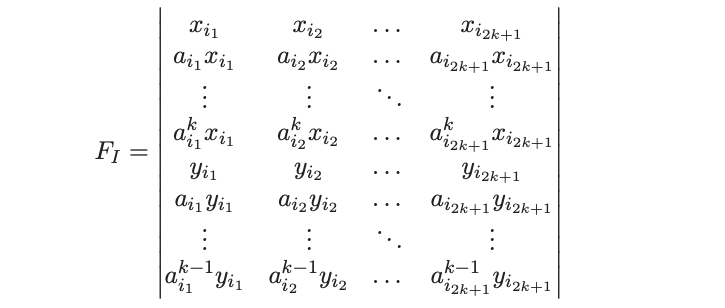Awards
National Science Foundation grants
- Personal grants
- 2024-2027. Novel Approaches to Geometry of Moduli Spaces, DMS-2401387
- 2021-2024. New Frontiers of Algebraic Geometry, DMS-2101726
- 2017-2021. Moduli Spaces: New Directions, DMS-1701704
- 2013-2017. Moduli Spaces of Curves and Surfaces, DMS-1303415 (and REU supplement DMS-1539510)
- 2010-2013. Geometry of Moduli Spaces of Curves and Surfaces, DMS-1001344
- 2007-2010. Geometry of Compact Moduli Spaces, DMS-0701191 (and REU supplement DMS-0827994)
- Conference grants
- 2009-2022. AGNES. Algebraic Geometry NorthEastern Series, DMS-0963853, DMS-1064426, DMS-1360543, DMS-1937705
- 2019, 2024. ELGA. Latin American School of Algebraic Geometry and Applications, DMS-1935081, DMS-2401164

Informal description of research interests
Preprints, papers and books on Algebraic Geometry
-
Noncommutative resolution of SUC(2), with E. Sink, 22p. (2024), arXiv:2405.08891
Lecture notes
(VBAC seminar)
Abstract.
We study the derived category of the moduli space SUC(2) of rank 2 vector bundles on a smooth projective curve C of genus g at least 2 with trivial determinant.
This generalizes the recent work by Tevelev and Torres on the case with fixed odd determinant.
Since SUC(2) is singular, we work with its resolution of singularities, specifically with the noncommutative resolution constructed by Padurariu and Spenko-Van den Bergh (in the more general setting of symmetric stacks). We show that this noncommutative resolution admits a semiorthogonal decomposition into derived categories of symmetric powers Sym2kC for 2k at most g-1. In the case of even genus, each block appears four times. This is also true in the case of odd genus, except that the top symmetric power Symg-1C
appears twice.
In the case of even genus, the noncommutative resolution is strongly crepant in the sense of Kuznetsov and categorifies the intersection cohomology of SUC(2).
Since all of its components are ``geometric,'' our semiorthogonal
decomposition provides evidence for the expectation, which dates back to the work of
Newstead and Tyurin, that SUC(2) is a rational variety.

-
Braid and Phantom, 45p. (2023), arXiv:2304.01825
Video introduction
(EDinburgh GEometry seminar)
Braid in genus two and variation of quantum cohomology (a short video)
Abstract.
Let N be the moduli space of stable rank 2 vector bundles on a smooth projective curve of genus g>1
with fixed odd determinant.
With Sebastian Torres, we previously found a semi-orthogonal decomposition of
the bounded derived category of N
into bounded derived categories of symmetric powers of the curve and, possibly,
a phantom block. In this work, we employ the theory of weaving patterns to eliminate the possibility of a phantom,
completing the proof of the decomposition
conjectured by Narasimhan and, independently, by Belmans, Galkin, and Mukhopadhyay.
-
Categorical aspects of the Kollár-Shepherd-Barron correspondence,
with G. Urzúa, 44p. (2022),
arXiv:2204.13225
Lecture notes (Algebra Seminar at UCLA)
Abstract.
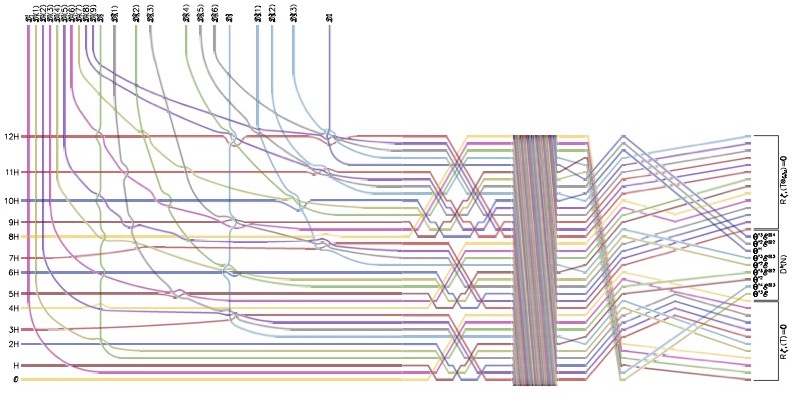
It is well known that a 2-dimensional cyclic quotient singularity W has the same singularity category as a finite dimensional associative algebra R introduced by Kalck and Karmazyn. We study the deformations of the algebra R induced by the deformations of the surface W to a smooth surface. We show that they are Morita--equivalent to path algebras R̂ of acyclic quivers for general smoothings within each irreducible component of the versal deformation space of W (as described by Kollár and Shepherd-Barron).
Furthermore, R̂ is semi-simple if and only if the smoothing is Q-Gorenstein (one direction is due to Kawamata).
We provide many applications. For example, we describe strong exceptional collections of length 10 on all Dolgachev surfaces and classify admissible embeddings of derived categories of quivers into derived categories of rational surfaces.
-
The BGMN conjecture via stable pairs,
with S. Torres,
to appear in Duke Math. Journal,
52p. (2021),
arXiv:2108.11951
Lecture notes (WAGS at Riverside)
Abstract.
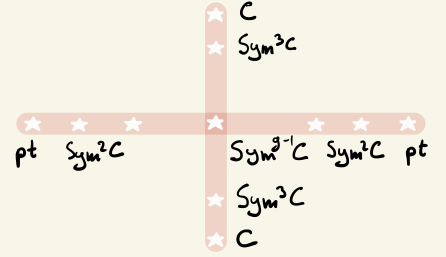
Let C be a smooth projective curve of genus g>1 and let N be the moduli space of stable rank 2 vector bundles on C of odd degree. We
construct a semi-orthogonal decomposition of the bounded derived category of N conjectured by Narasimhan and by Belmans, Galkin and Mukhopadhyay.
It has two blocks for each i-th symmetric power of C for i=0,...,g-2 and one block for the (g-1)-st symmetric power.
We conjecture that the subcategory generated by our blocks has a trivial semi-orthogonal complement,
proving the full BGMN conjecture. Our proof is based on an analysis of wall-crossing between moduli spaces of stable pairs,
combining classical vector bundles techniques with the method of windows.
-
Blown-up toric surfaces with non-polyhedral effective cone,
with A.-M. Castravet,
A. Laface and
L. Ugaglia,
Crelle's Journal (2023), vol. 2023, no. 800, pp. 1-44
Lecture video (Seminario de Geometria Algebraica, Universidad Catolica de Chile)
Abstract.
We construct projective toric surfaces whose blow-up
at a general point has a non-polyhedral
pseudo-effective cone.
As a consequence, we prove that the pseudo-effective cone
of the Grothendieck--Knudsen moduli space M0,n of stable rational curves is not polyhedral
for n≥10. These results hold both in characteristic 0
and in characteristic p, for all primes p.
Many of these toric surfaces are related to an interesting
class of arithmetic threefolds that we call arithmetic
elliptic pairs of infinite order. Their analysis relies on tools of arithmetic geometry and Galois representations in the spirit of the Lang--Trotter conjecture, producing toric surfaces whose blow-up at a general point has a non-polyhedral
pseudo-effective cone in characteristic 0 and in characteristic p, for an infinite set of primes p of positive density.

-
Scattering amplitudes of stable curves,
to appear in Geometry and Topology,
54 p. (2020), arXiv:2007.03831
Lecture notes (Geometry Seminar at UT Austin)
Abstract. Equations of hypertree divisors on the Grothendieck-Knudsen moduli space of stable rational curves, introduced by Castravet and Tevelev, appear as numerators of scattering amplitude forms for n massless particles in N=4 Yang-Mills theory in the work of Arkani-Hamed, Bourjaily, Cachazo, Postnikov and Trnka. Rather than being a coincidence, this is just the tip of the iceberg of an exciting relation between algebraic geometry and high energy physics. We interpret scattering amplitude forms as probabilistic Brill-Noether theory: the study of statistics of images of n marked points under a random meromorphic function uniformly distributed with respect to the translation-invariant volume form of the Jacobian. We focus on the maximum helicity violating regime, which leads to a beautiful physics-inspired geometry for various classes of algebraic curves: smooth, stable, hyperelliptic, real algebraic, etc.

-
Derived category of moduli of pointed curves - II,
with A.-M. Castravet,
70 p. (2020), arXiv:2002.02889
Abstract.
We prove the Manin-Orlov conjecture: the moduli space of stable rational curves with n marked points has a full exceptional collection equivariant under the action of the symmetric group Sn permuting the marked points. In particular, its K-group with integer coefficients is a permutation Sn-lattice.
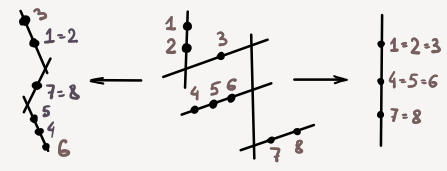
-
Compactifications of moduli of points and lines in the projective plane,
with L. Schaffler,
International Mathematics Research Notices (2022), Issue 21, 17000--17078
Lecture video and
Lecture notes (Tropical Geometry in Zoom Seminar)
Abstract. Projective duality identifies moduli spaces
of points in P2 and lines in the dual
P2.
The latter space admits Kapranov's Chow quotient compactification, studied also
by Lafforgue, Hacking, Keel, Tevelev, and Alexeev,
which gives an example of a KSBA moduli space of stable surfaces:
it carries a family of reducible degenerations of P2 with
"broken lines". Gerritzen and Piwek proposed a dual perspective, a compact moduli space
parametrizing reducible degenerations of P2 with n smooth points. We investigate
the relation between these approaches, answering a question of Kapranov from 2003.
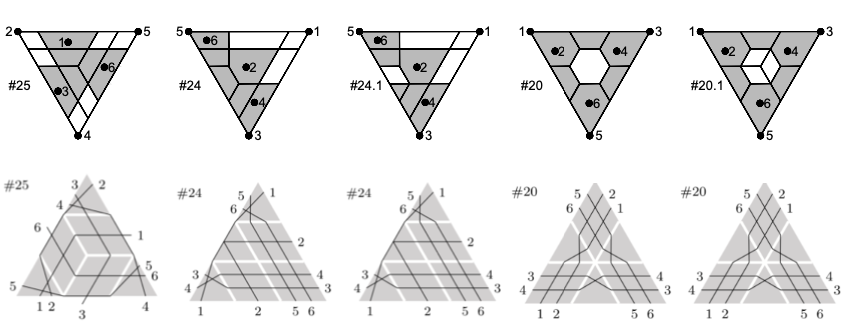
-
Spherical Tropicalization
with A. Vogiannou,
Transformation Groups 26 (2021), 691-718 (Ernest Vinberg memorial volume)
Abstract. We extend tropicalization and tropical compactification of subvarieties of algebraic tori to subvarieties of spherical homogeneous spaces. Given a tropical compactification of a subvariety, we show that the support of the colored fan of the ambient spherical variety agrees with the tropicalization of the subvariety. The proof is based on our equivariant version of the attening by blow-up theorem. We provide many examples.
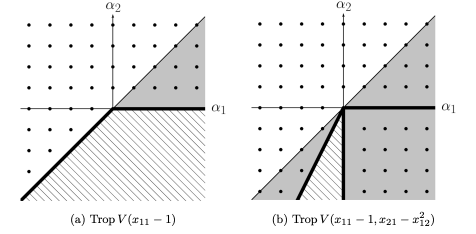
-
Exceptional collections on certain Hassett spaces,
with A.-M. Castravet, Épijournal de
Géométrie Algébrique 4 (2020), 1-34
Abstract. We construct an S2xSn
invariant full exceptional collection on Hassett spaces of weighted stable rational curves with
n+2 markings and weights (1/2+a,1/2+a,b,...,b), for very small positive a,b,
that can be identified with symmetric GIT quotients of (P1)n by the diagonal action of Gm when n is odd, and their Kirwan desingularization when n is even. The existence of such an exceptional collection is one of the needed ingredients in order to prove the existence of a full Sn-invariant exceptional collection on the moduli space of stable rational curves with n marked points . To prove exceptionality we use the method of windows in derived categories. To prove fullness we use previous work on the existence of invariant full exceptional collections on Losev-Manin spaces.

-
Derived category of moduli of pointed curves - I,
with A.-M. Castravet,
Algebraic Geometry 7 (6) (2020), 722-757
Abstract. This is the first paper in the sequence devoted to derived category of moduli spaces of curves of genus 0 with marked points. We develop several approaches to describe it equivariantly with respect to the action of the symmetric group permuting marked points. We construct an equivariant full exceptional collection on the Losev-Manin space which categorifies derangements.
-
The Craighero-Gattazzo surface is simply-connected,
with
J. Rana
and
G. Urzúa, Compositio,
153 (2017), 557-585
Abstract.
We show that the Craighero-Gattazzo surface, the minimal resolution of an explicit complex quintic surface with four elliptic singularities, is simply-connected. This was conjectured by Dolgachev and Werner, who proved that its fundamental group has a trivial profinite completion. The Craighero-Gattazzo surface is the only explicit example of a smooth simply-connected complex surface of geometric genus zero with ample canonical class. We hope that our method will find other applications: to prove a topological fact about a complex surface we use an algebraic reduction mod p technique and deformation theory.

-
Flipping Surfaces,
with P. Hacking and
G. Urzúa, Journal of Algebraic Geometry, 26 (2017), 279-345
Abstract.
We study semistable extremal threefold neighborhoods following earlier work of Mori, Kollár, and Prokhorov. We classify possible flips and extend Mori's algorithm for computing flips of extremal neighborhoods of type k2A to more general neighborhoods of type k1A. In fact we show that they belong to the same deformation family as k2A, and we explicitly construct the universal family of extremal neighborhoods. This construction follows very closely Mori's division algorithm, which we interpret as a sequence of mutations in the cluster algebra of rank 2 with general coefficients. We identify, in the versal deformation space of a cyclic quotient singularity, the locus of deformations such that the total space admits a (terminal) antiflip. We show that these deformations come from at most two irreducible components of the versal deformation space. As an application, we give an algorithm for computing stable one-parameter degenerations of smooth projective surfaces (under some conditions) and describe several components of the Kollár-Shepherd-Barron boundary of the moduli space of smooth canonically polarized surfaces of geometric genus zero.
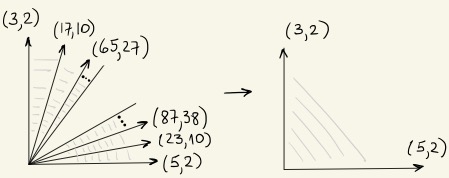
-
M
0,n is not a Mori Dream Space,
with A.-M. Castravet,
Duke Math. Journal, 164, no. 8 (2015), 1641-1667
Abstract.
Building on the work of Goto, Nishida and Watanabe on symbolic Rees algebras of monomial primes, we prove that the moduli space of stable rational curves with n punctures is not a Mori Dream Space for n>133. This answers the question of Hu and Keel.
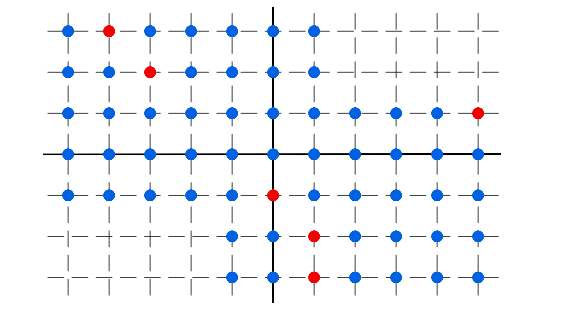
-
On a Question of Teissier,
Collectanea Math., 65, no. 1 (2014), 61-66
Abstract.
We answer positively a question of B. Teissier on existence of resolution of singularities inside an equivariant map of toric varieties.

-
Hypertrees, Projections, and Moduli of Stable Rational Curves
,
with A.-M. Castravet,
Crelle's Journal, 675 (2013), 121-180.
A database of hypertree divisors by Scheidwasser and Opie.
Abstract.
We give a description for the subcone of effective divisors of the Grothendieck-Knudsen moduli space of stable rational curves with n marked points. Namely, we introduce new combinatorial structures called hypertrees and show they give exceptional divisors with many remarkable properties.
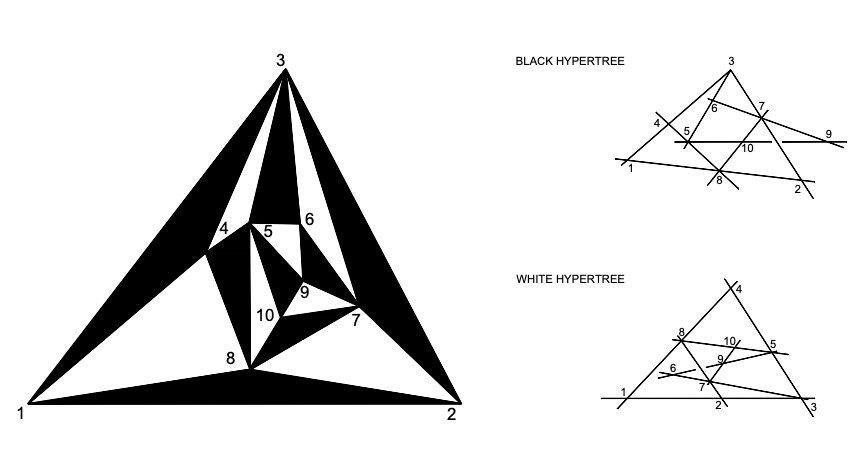
-
Rigid Curves on M
0,n and Arithmetic Breaks
,
with A.-M. Castravet, Contemporary Math., 564 (2012), 19-67
Abstract.
A result of Keel and McKernan states that a hypothetical counterexample to the F-conjecture must come from rigid curves on the moduli space of
stable rational curves that intersect the interior. We exhibit several ways of constructing rigid curves. In all our examples, a reduction mod p argument shows that the classes of the rigid curves that we construct can be decomposed as sums of F-curves.
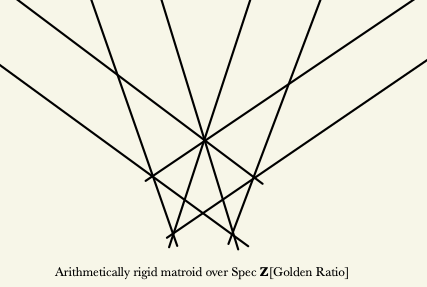
-
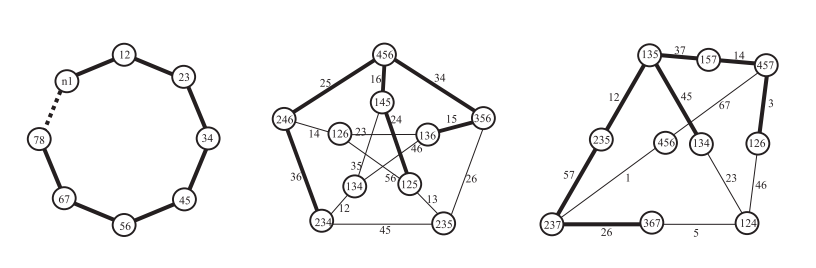
Stable Pair, Tropical, and Log Canonical Compact Moduli of Del Pezzo Surfaces,
with P. Hacking and
S. Keel,
Inventiones Math. 178 , no.1 (2009), 173-228
Abstract.
We give a functorial normal crossing compactification of the moduli of smooth marked cubic surfaces entirely analogous to the Grothendieck-Knudsen moduli space
of stable rationale curves.
-
Equations for M
0,n, with S. Keel,
International Journal of Math. 20, no.9 (2009), 1--26
Abstract.
We show that the log canonical bundleof the moduli space of stable rational curves is very ample, show the homogeneous coordinate ring is Koszul,
and give a nice set of rank 4 quadratic generators for the homogeneous ideal: The embedding is equivariant for the symmetric group, and the image lies on many Segre embedded copies of P1xP2x...xPn-3, permuted by the symmetric group. The homogeneous ideal of the moduli space
is the sum of the homogeneous ideals of these Segre embeddings.
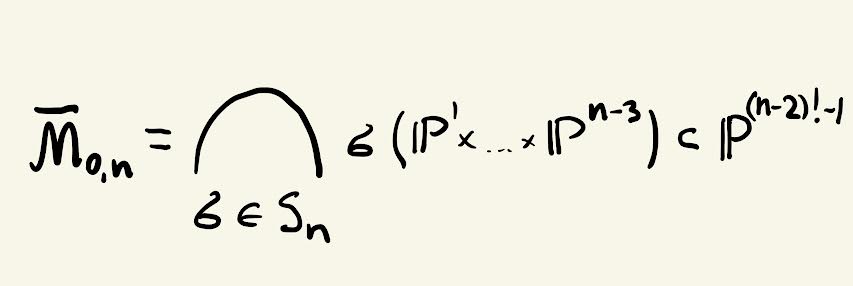
-
Exceptional Loci on M
0,n and Hypergraph Curves
,
with A.-M. Castravet, 39p (2008), arXiv:0809.1699
This preprint was superseded by [21] and [22]. It is not intended for publication.
-
Elimination Theory for Tropical Varieties,
with B. Sturmfels,
Math. Research Letters 15, no.3 (2008), 543-562
Abstract.
Tropical algebraic geometry offers new tools for elimination theory and implicitization. We determine the tropicalization of the image of a subvariety of an algebraic torus under any homomorphism from that torus to another torus.
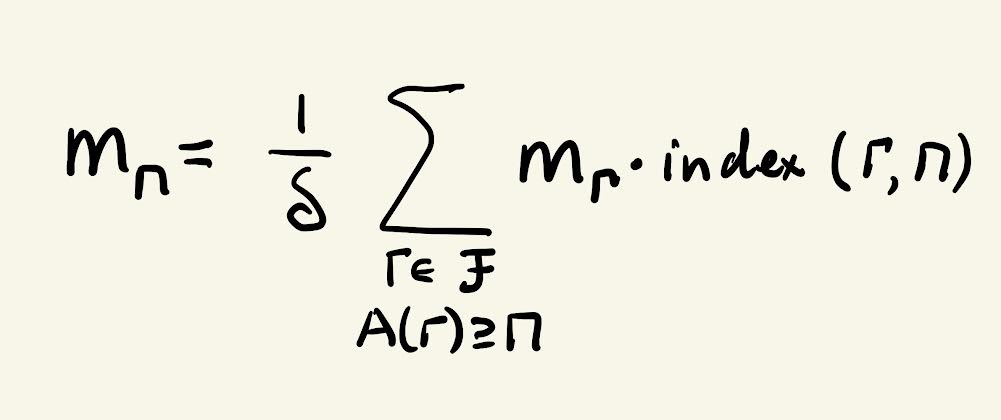
-
The Newton Polytope of the Implicit Equation,
with B. Sturmfels and
J. Yu,
Moscow Math. Journal 7, no.2 (2007), 327-346
Abstract.
We apply tropical geometry to study the image of a map defined by Laurent polynomials with generic coefficients. If this image is a hypersurface then our approach gives a construction of its Newton polytope.

-
Compactifications of Subvarieties of Tori,
American Journal of Math. 129, no. 4 (2007), 1087-1104
Abstract.
We study compactifications of subvarieties of algebraic tori defined by imposing a sufficiently fine polyhedral structure on their non-archimedean amoebas. These compactifications have many nice properties, for example any k boundary divisors intersect in codimension k. We consider some examples including the moduli space of stable
rational curves (and more generally log canonical models of complements of hyperplane arrangements) and compact quotients of
Grassmannians by a maximal torus.
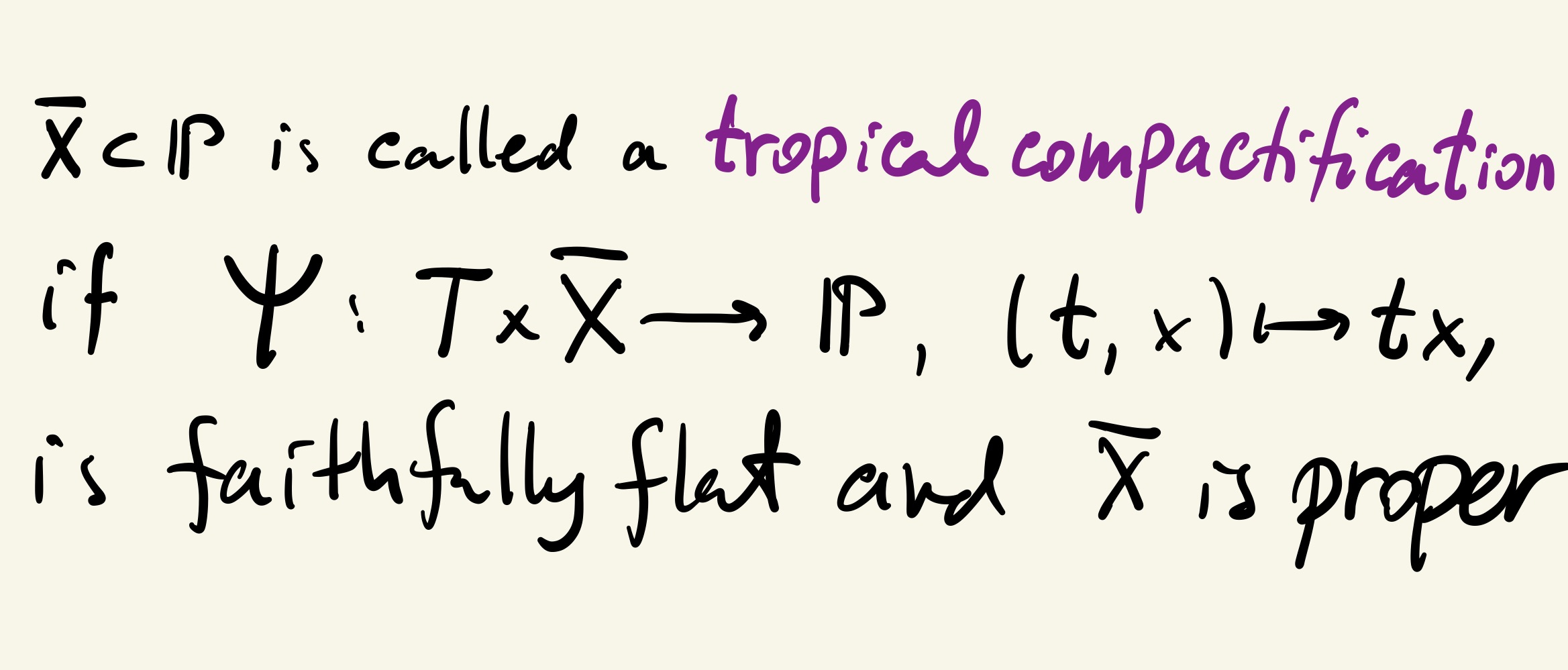
-
Compactification of the Moduli Space of Hyperplane Arrangements,
with P. Hacking and S. Keel,
Journal of Algebraic Geometry 15 (2006), 657-680
Abstract.
Consider the moduli space M0 of arrangements of n hyperplanes in general position in projective (r-1)-space. When r=2 the space has a compactification given by the moduli space of stable curves of genus 0 with n marked points. In higher dimensions, the analogue of the moduli space of stable curves is the moduli space of stable pairs: pairs (S,B) consisting of a variety S (possibly reducible) and a divisor B=B1+...+Bn satisfying various additional assumptions. We identify the closure of M0 in the moduli space of stable pairs as Kapranov's Chow quotient compactification of M0, and give an explicit description of the pairs at the boundary. We also construct additional irreducible components of the moduli space of stable pairs.
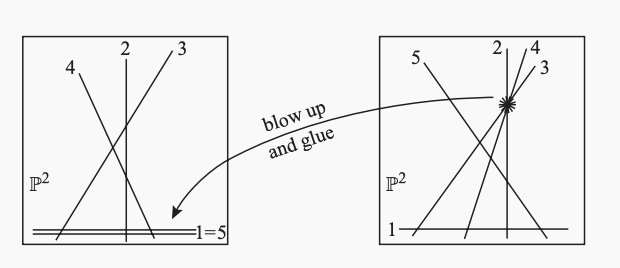
-
Hilbert's 14-th Problem and Cox Rings,
with A.-M. Castravet, Compositio 142 (2006), 1479-1498
Abstract.
Our main result is the description of generators of the total coordinate ring of the blow-up of Pn in any number of points that lie on a rational normal curve. As a corollary we show that the algebra of invariants of the action of a two-dimensional vector group introduced by Nagata is finitely generated by certain explicit determinants. We also prove the finite generation of the algebras of invariants of actions of vector groups related to T-shaped Dynkin diagrams introduced by Mukai.
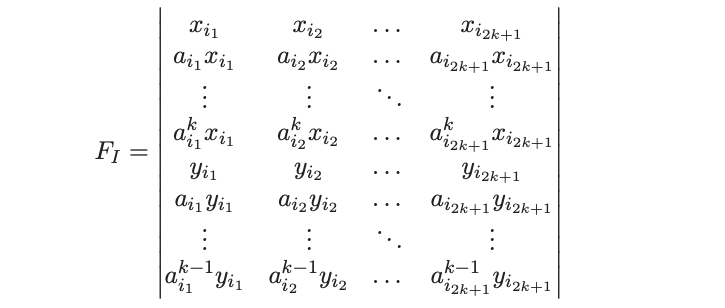
-
Geometry of Chow Quotients of Grassmannians,
with S. Keel,
Duke Math. Journal 134, no. 2 (2006), 259-311
Abstract.
We consider Kapranov's Chow quotient compactification of the moduli space of ordered n-tuples of hyperplanes in Pr-1
in linear general position. For r=2 this is canonically identified with the Grothendieck-Knudsen moduli space of stable rational curves
which has among others the nice properties 1) Modular meaning: stable pointed rational curves 2) Canonical description of limits of one parameter degenerations 3) Natural Mori theoretic meaning: log canonical compactification. We prove (1-2) generalize naturally to all (r,n), but that (3), which we view as the deepest, fails except possibly in the cases (2,n),(3,6),(3,7),(3,8), where we conjecture it holds.
Update.
The conjecture was proved by Luxton-Qu (3,6),
Corey (3,7), Corey-Luber (3,8).
-
Projective Duality and Homogeneous Spaces,
Springer 2005
Abstract.
For several centuries, various reincarnations of projective duality have inspired research in algebraic
and differential geometry, classical mechanics, invariant theory, combinatorics, etc. On the other hand,
projective duality is simply a systematic way of recoveringthe projective variety from the set of its tangent
hyperplanes. In this survey we have tried to collect together different aspects of projective duality and
points of view on it. We hope, that the exposition is quite informal and requires only a standard knowledge
of algebraic geometry and algebraic (or Lie) group theory. Some chapters are, however, more difficult and
use the modern intersection theory and homology algebra. But even in these cases we have tried to give
simple examples and avoid technical difficulties.
Older papers on Transformation Groups and Invariant Theory