Letters of recommendation
I follow Ravi Vakil's rules on letters of recommendation
Please read them before requesting a letter.
Research and training program in Undergraduate Algebraic Geometry
Postdocs
Graduate students
-
Anibal Aravena
- Sebastian Torres,
Windows in Algebraic Geometry and Applications to Moduli
Click to see the research description
Sebastian applied the theory of windows, as developed by Teleman, Halpern-Leistner,
and by Ballard, Favero and Katzarkov, to study certain moduli spaces and their derived categories. Using quantization and other techniques, he proved that
GIT quotients of (P1)n by PGL2
without strictly semistable points satisfy a rare property called Bott vanishing, which states that Ω jY⊗L has no higher cohomology for every j and every ample line bundle L. Previously this was known only for n=5 due to a result of Totaro. Similar techniques are used in the thesis to reprove the well known fact that toric varieties satisfy Bott vanishing. Sebastian also used the theory of windows to explore derived categories of moduli spaces of rank-two vector bundles on a curve. By applying these methods to Thaddeus' moduli spaces, he found a four-term sequence of semi-orthogonal blocks in the derived category of the moduli space of rank-two vector bundles on a curve of genus at least 3 and determinant of odd degree, a result in the direction of the Narasimhan conjecture.
-
Arie Stern Gonzalez,
Anticanonical Models of Smoothings of Cyclic Quotient Singularities
Click to see the research description
Arie studied anticanonical models of smoothings of cyclic quotient singularities.
Given a surface cyclic quotient singularity Y, it is an open problem to
determine all smoothings of Y that admit an anticanonical model and to compute
it. In [25], Hacking, Tevelev and Urzua studied certain irreducible components
of the versal deformation space of Y , and within these components, they found
one parameter smoothings of Y that
that admit an anticanonical model and proved
that the total spaces have canonical singularities. Moreover, they compute explicitly the anticanonical models that have terminal singularities using Mori's division algorithm. Arie studied one parameter smoothings in these components that admit an
anticanonical model with canonical but non-terminal singularities with the goal of
classifying them completely. He identified certain class of "diagonal" smoothings
(smoothings with equal axial multiplicities),
where the total space is a toric threefold and constructed the anticanonical model
explicitly using the toric MMP.
-
Tassos Vogiannou, Spherical Tropicalization
Click to see the research description
In his thesis, Tassos extended the theory of tropicalization and tropical compactifications
of subvarieties of algebraic tori from
[15]
to subvarieties of spherical homogeneous spaces. He showed the existence of tropical compactifications in a general setting. Given a tropical compactification of a closed subvariety of a spherical homogeneous space, he showed that the support of the colored fan of the ambient spherical variety agrees with the tropicalization of the closed subvariety. He provided many examples of tropicalization of subvarieties of GL(n), SL(n), and PGL(n).
-
Julie Rana,
Boundary Divisors in the Moduli Space of Stable Quintic Surfaces
Click to see the research description
Julie found a bound on which singularities may appear on KSBA stable surfaces for a wide range of topological invariants, and used this result to describe all stable numerical quintic surfaces, i.e. stable surfaces with K2= 5, pg=4, and q=0, whose unique non Du Val singularity is a Wahl singularity. Quintic surfaces are the simplest examples of surfaces of general type and the question of describing their moduli is a long-standing question in algebraic geometry. Julie extended the deformation theory of Horikawa to the log setting in order to describe the boundary divisor of the moduli space of KSBA stable numerical quintic surfaces corresponding to these surfaces.
Research and training program in Undergraduate Algebraic Geometry
Since 2007, a rigorous year-long training program has been established and supported by the National Science Foundation and internal grants.
Click to see the program description
The program is open to motivated undergraduate students who are interested in pursuing a career in STEM. Those who are interested in participating are encouraged to apply in December by submitting their CV, unofficial transcript, and a statement of interest.
Applicants who have taken graduate courses or are from groups underrepresented in STEM will receive preference during the selection process. The program kicks off in the Spring semester with a comprehensive reading course on algebraic geometry. Following that, the students will engage in a Research Experience for Undergraduates (REU) in the summer.
In the Fall semester, the program offers another independent study to help students concentrate on their writing skills and complete either an Honors thesis or a paper. The program also provides support and guidance for graduate school and scholarship applications, along with mentoring to help students achieve their career goals. Overall, this program offers a comprehensive and in-depth training experience that is tailored to the unique needs of each individual student.
As a Math Alliance mentor , I support underrepresented undergraduate students in pursuing doctoral studies in math. I offer guidance, personalized mentoring, and connect them to resources and opportunities to develop their skills and succeed in their field.
Advice for UMass undergraduate students pursuing research in pure mathematics
Current program participants and alumni
(for citations see the research page)
-
Sam Silver studies birational geometry of the moduli space of stable rational curves.
-
Aditya Khurmi,
Toric Elliptic Pairs with Picard Number Three
Click to see the research description
An elliptic pair (X,C) is a generalization of a rational elliptic fibration X→P1
with fiber C, introduced in [33].
Here, X is a projective rational surface with log terminal singularities, and C is an irreducible curve contained in the smooth locus of X, with pa(C)=1 and C2=0. These naturally arise as blowups X:=Ble(PΔ) of projective toric surfaces, whose Newton polygon is elliptic. The order of O(C)|C in Pic0(C) gives a quantitative way to check if X is an elliptic fibration, which is equivalent to finiteness of the order. We call Δ a Lang-Trotter polygon when this order is infinite, in which case Eff(Ble(PΔ)) is non-polyhedral. Results of
Elizabeth Pratt show there are exactly 3 elliptic triangles up to SL(Z), none of which is Lang-Trotter. The paper [33]
gives an infinite family of Lang-Trotter pentagons and heptagons, and various examples of other polygons when ρ(PΔ)>2. Remark 4.7 in the paper asks if any Lang-Trotter quadrilaterals exist, and Aditya answers this in the negative by studying the curves in the Zariski Decomposition of KX+C.
- Elias Sink, Moduli spaces of line configurations and vector bundles
Click to see the research description
Line configurations and K3 surfaces.
Configurations of lines in P2 over various fields have been studied since the 19th century. Particularly fascinating are n3 configurations, which consist of n points and n lines, with each line containing exactly 3 points and each point lying on 3 lines. An example is the Fano configuration, a 73 configuration. A classical question is: Which configurations are realizable over Q? This query is directly related to the modern study of rational points on Calabi-Yau varieties. It has been shown that the realization space of an n3 configuration, constructed as a GIT quotient with democratic polarization, is a Calabi-Yau variety (potentially singular) if it has the expected dimension of n-8. In his paper, Elias Sink has completed the K3 surface case (n=10). There are exactly 10 such configurations, including the Desargues configuration, where the nine collinearities imply the tenth, according to Desargues' theorem, thus making the realization space three-dimensional. There is also a unique non-realizable configuration. Among the rest, four configurations' GIT quotient is a reducible Kulikov degeneration of a K3 surface. Finally, four configurations yield beautiful smooth K3 surfaces with a Picard number of 20. Answering a question posed by Sturmfels in 1991, Elias proves that their realizations over Q are dense in those over R. These K3 surfaces can be precisely identified, including the universal elliptic curve over Γ1(7).
Noncommutative resolution of SUC(2). We study the derived category of the moduli space SUC(2) of rank 2 vector bundles on a smooth projective curve C of genus g at least 2 with trivial determinant.
This generalizes the recent work by Tevelev and Torres on the case with fixed odd determinant.
Since SUC(2) is singular, we work with its resolution of singularities, specifically with the noncommutative resolution constructed by Padurariu and Spenko-Van den Bergh (in the more general setting of symmetric stacks). We show that this noncommutative resolution admits a semiorthogonal decomposition into derived categories of symmetric powers Sym2kC for 2k at most g-1. In the case of even genus, each block appears four times. This is also true in the case of odd genus, except that the top symmetric power Symg-1C
appears twice.
In the case of even genus, the noncommutative resolution is strongly crepant in the sense of Kuznetsov and categorifies the intersection cohomology of SUC(2).
Since all of its components are ``geometric,'' our semiorthogonal
decomposition provides evidence for the expectation, which dates back to the work of
Newstead and Tyurin, that SUC(2) is a rational variety.
Elias will continue his studies at the PhD program in Harvard with the NSF graduate research fellowship (GRFP).
- Pranav Ramakrishnan, The Arithmetic of Elliptic Pairs and An (n+1)-variable Artin Conjecture
Click to see the research description
Pranav studied the density of polyhedral primes for blow-ups of P2. The theory of elliptic pairs, as investigated in the paper [33], provides useful conditions to determine the polyhedrality of the pseudo-effective cone. These conditions lead to intriguing arithmetic questions when reducing the variety modulo p. In his paper The Arithmetic of Elliptic Pairs and An (n+1)-variable Artin Conjecture, Pranav examines a specific case: the blow-up X of 9 points in P2 lying on a nodal cubic. He studies the density of primes p for which the pseudo-effective cone of the reduction of X modulo p is polyhedral. This problem is can be reduced to an analogue of Artin's Conjecture on primitive roots, as previously explored by Stephens and later by Moree and Stevenhagen. Pranav's findings show that the density of such "polyhedral primes" approximates a higher analogue of Stephens' Constant, contingent on the assumption of the Generalized Riemann Hypothesis. To determine a precise value for the density of polyhedral primes, he examines the containment of rank 8 root sublattices in E8.
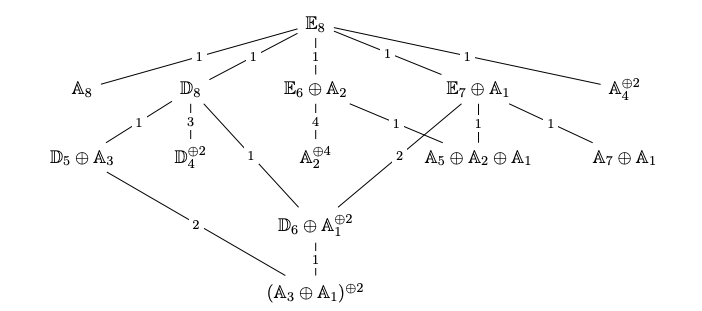
Pranav will continue his studies at the PhD program at Boston College.
- Viviene Do studied scattering amplitudes of stable M-curves of genus 1 and 2, see [32]
- Elizabeth Pratt,
The Geometry Of Elliptic Pairs
Click to see the research description
Elizabeth studied toric elliptic pairs (as detailed in [33]). An elliptic pair (X, C) is a projective rational surface X with log terminal singularities, and an irreducible curve C contained in the smooth locus of X, with arithmetic genus 1 and self-intersection 0. These pairs are valuable for determining whether the pseudo-effective cone of X is polyhedral, and they are interesting algebraic and geometric objects in their own right. Particularly notable are toric elliptic pairs, where X is the blow-up of a projective toric surface at the identity element of the torus. In her paper The Geometry Of Elliptic Pairs, published in J. Pure Appl. Algebra (2023), Elizabeth classified all toric elliptic pairs of Picard number 2. Remarkably, only three such pairs exist. Additionally, she explored a class of non-toric elliptic pairs arising from the blow-up of P2 at nine points on a nodal cubic, in characteristic p. This study reveals examples of surfaces where the pseudo-effective cone is non-polyhedral for a set of primes p of positive density, and, under the assumption of the generalized Riemann hypothesis, polyhedral for a set of primes p of positive density.
Elizabeth is currently a graduate student at UC Berkeley, holding an NSF graduate research fellowship (GRFP).
-
Shelby Cox,
Equations for the log canonical model of hyperplane arrangement complement
Click to see the research description
Shelby explored log canonical models of hyperplane arrangement complements, with a particular focus on the braid arrangement (as discussed in [19] and [15]). She developed an Honors Thesis on this subject.
Shelby's research contributions have been recognized with the UMass Rising Researcher award.
Shelby earned her PhD from the University of Michigan
with the NSF Graduate Research Fellowship (GRFP).
She is currently a a postdoc in the Non-Linear Algebra Group at the Max Planck Institute for Mathematics in the Sciences.
- Greg McGrath,
Seshadri Constants on Irrational Surfaces
Click to see the research description
Greg studied Seshadri constants on irrational surfaces. An interpolation problem is a challenge in which the goal is to find a geometric object that passes through a set of sufficiently general points with specified multiplicities. These types of questions trace back to the fundamentals of geometry, as exemplified by Euclid's postulation that a line can be drawn through any two points. Despite the fundamental nature of such questions, our understanding of polynomial interpolation remains limited. For curves in P2, Nagata's Conjecture offers a good prediction, although a proof is still elusive. In exploring interpolation on more complex varieties, an interesting avenue is computing Seshadri constants, which quantify the maximum multiplicity an irreducible curve can have at a particular general point. Greg authored an Honors Thesis on the Seshadri constants of the symmetric square of an elliptic curve. More recent developments related to this topic can be found in the paper Effective cone of the blow up of the symmetric product of a curve by A. Laface and L. Ugaglia.
Greg is currently a graduate student at UC Santa Barbara.
- Stephen Obinna,
Effective cones of blow-ups of toric surfaces
Click to see the research description
Stephen studied effective cones of blow-ups of toric surfaces at the identity element of the torus (as discussed in [24]). While examples of toric surfaces of Picard number 3, whose blow-ups at the identity element have a non-polyhedral effective cone, were later constructed (see [33]), the case of Picard number 2, which Stephen investigated, remains unresolved. He created an online database of these surfaces, featuring numerous curves with points of high multiplicity.
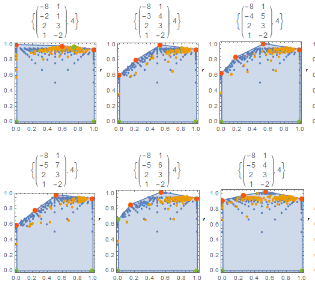
Stephen earned his PhD from Brown University. He is currently a Postdoctoral Fellow at the University of Waterloo.
- Morgan Opie,
Extremal divisors on M0,n
Click to see the research description
Morgan focused her studies on effective divisors on M0,n and authored a paper titled Extremal divisors on M0,n, published in the Michigan Math. J., V. 65(2) (2016), pages 251-285. In this work, she identified a counterexample to an overly optimistic conjecture from [22], also discussed in [33]. Morgan developed an online database of hypertree divisors, extending the earlier work by Ilya Scheidwasser (see [32]).
Morgan's achievements have been recognized with several awards, including the Churchill Scholarship and the UMass Rising Researcher award. Morgan was also a runner-up for the Alice T. Schafer Prize, a national award for excellence in mathematics by an undergraduate woman.
Morgan earned her PhD from Harvard
with the
NSF graduate research fellowship (GRFP)
and is currently a Hedrick Assistant Adjunct Professor and NSF Postdoc at UCLA.
- Nicky Reyes,
Extremal P-resolutions of cyclic quotient singularities
Click to see the research description
Nicky focused his research on extremal P-resolutions of cyclic quotient singularities, verifying a conjecture (later proven and discussed in [25]) that these resolutions occur in pairs, at most.
Nicky earned his PhD degree from the University of Texas at Austin with the NSF graduate research fellowship (GRFP). He is currently employed at UT Austin as an Assistant Professor of Instruction.
-
Nate Harman, Combinatorics of hypertrees
Click to see the research description
Nate focused his research on the combinatorics of hypertrees, contributing several significant findings to the paper [22].
Nate earned his PhD degree from MIT with the NSF graduate research fellowship (GRFP). Nate is an
Assistant Professor at the University of Georgia.
-
Charles Boyd, Q-Gorenstein degenerations of the Craighero-Gattazzo surface
Click to see the research description
Charles made a pivotal contribution to the paper [26] by discovering a Q-Gorenstein degeneration of the Craighero-Gattazzo surface into a surface with a Wahl singularity in characteristic 7.
Charles completed an internship at Macaulay 2, a computer algebra system, and is currently employed as a Systems Software Developer at cPanel.
-
Ilya Scheidwasser,
Hypergraph curves
Click to see the research description
Ilya conducted studies on hypergraph curves and hypertrees, as referenced in [22] and [32]. He authored a Capstone thesis on these topics and also developed a C++ program that successfully identified all hypertrees with 7, 8, 9, 10, and 11 vertices.
Ilya received his PhD degree from Northeastern University and is currently a Principal Software Developer at athenahealth.
-
Alex Levin, Boundary complex of the Naruki space
Click to see the research description
Alex focused his research on the dual complex of the boundary of the Naruki moduli space of cubic surfaces, as discussed in [20]. He successfully proved that this complex is shellable.
Alex received his PhD degree from the University of New Hampshire and is currently serving as a lecturer at the University of Vermont.
