go straight to the plots (please read this page first)
Approximations of the effective cones of blow ups X of some toric surfaces S with picard number 2. Specifically, we approximate the preimage C in Eff(X) of the nef cone of S.
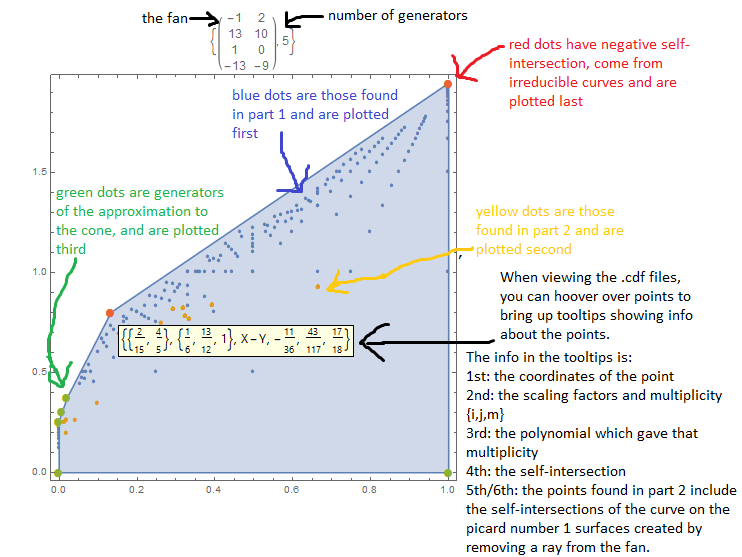
Part 1: For each fan, I generate several normal polygons corresponding to different polarizations of a toric surface S (parameterized by the lengths of 2 consecutive sides) and for each polygon I calculate the maximum multiplicity (at {1,1}) of a polynomial with Newton polygon contained in the polygon, giving a set of points {i,j,m} where {i,j} are the parameters that determine the polygon and m is the maximum multiplicity. The points {i,j,m} belong to C.
Part 2: Then, for each of the points found in C, I look at the polynomial giving the maximum multiplicity, and for each of its irreducible factors I find the smallest polygon normal to the fan containing this polynomial and this gives more points in C. The convex hull of all these points gives an approximation of C, and I plot the crossection cut out by "i+j=1".
I used this code to turn fans into text files of data and then this code to turn that data into the plots.
The approximations to C are represented by plots that look like the one below:
Toric varieties are basic examples of Mori Dream Spaces but their blow-ups in the identity element of the torus can fail to be Mori Dream Spaces (see [Castravet-Tevelev], [Gonzalez-Karu], [Hausen-Keicher-Laface]). Specifically, in all known examples one can find a nef divisor which is not semi-ample. A blow-up of a toric surface can potentially fail to be a MDS in two other ways: one of the faces of the nef cone can have an irrational slope or the effective cone can fail to be finitely generated. However, no examples of these types are known. It is conjectured that the blow-up of the weighted projective plane P(9,10,13) (and some others) give examples of the first type but proving this is extremely difficult due to relation to Nagata's approximation conjecture. Professor Jenia Tevelev conjectures that there exists a toric surface for which the effective cone of the blow-up is not finiteley generated, which will provide an example of the other type. The hope is that finding examples with a large numbers of generators may shed some light on the problem and identify potential examples.