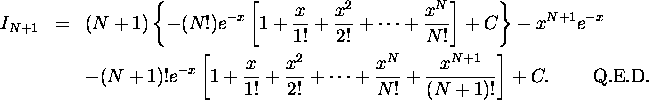Math 431 Section 4 Solution of problem 31 in section 3.5
(a) We verify that the function 
is a solution of
by plugging in.
(b) We find the general solution using the method of reduction of order.
Postulate a solution of the form 
.
Plugging 
into the normalized equation (in
the form y''+p(x)y'+q(x)y=0)
and using the fact that
is a solution, we get that
v'(x) satisfies the differential equation:
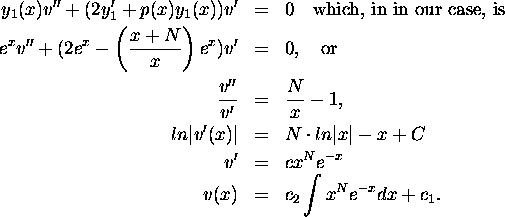
So, the general solution is:
(c) We claim that the integral 
below satisfies the following equality:
Consequently, choosing 
in (1)
we see that 
is a polynomial solution of our
differential equation. Since you are given the anti-derivative in
(2) you can verify (2)
simply by differentiating both sides. Alternatively, one can
evaluate (2) recursively with repect to N:
Case N=1: Use integration by parts:
General N:
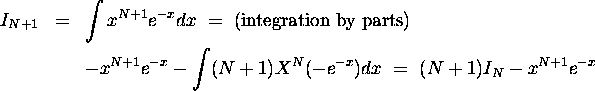
From the last equality it is easy to guess the general form of the integral in (2) and prove it by induction. The case N=1 was proven. We assume that (2) holds for N and prove it for N+1:
