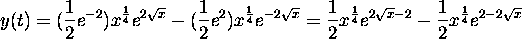![]()
where ![]() is the
general solution of the associated homogeneous equation.
is the
general solution of the associated homogeneous equation.
![]() ,
, ![]() ,
are particular solutions of
,
are particular solutions of ![]() found via the
method of undetermined coefficients. For
found via the
method of undetermined coefficients. For ![]() we look for a solution of
the form
we look for a solution of
the form ![]() . Plugging in we find that
. Plugging in we find that
![]() . Equating coefficients we get
. Equating coefficients we get
![]() . For
. For ![]() we look for a solution of
the form
we look for a solution of
the form ![]() . Plugging in we find that
. Plugging in we find that ![]() . For
. For
![]() we look for a solution of
the form
we look for a solution of
the form ![]() because 2 is a root
of the characteristic equation with multiplicity 1. Plugging in we get:
because 2 is a root
of the characteristic equation with multiplicity 1. Plugging in we get:
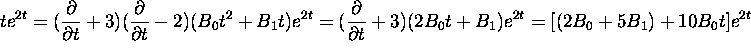 Equating coefficients we get the two equations
Equating coefficients we get the two equations
![]() and
and ![]() . Hence,
. Hence, ![]() and
and
![]() . The general solution is
. The general solution is
![]()
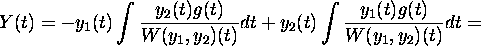
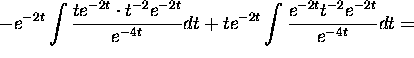
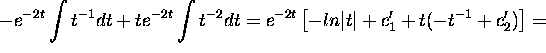
![]()
with initial condition ![]() and
and ![]() .
.
- (2 points)
If the mass weighs
 , then
, then 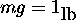 .
Hence, the mass stretches the spring L feet where L satisfies the equation
.
Hence, the mass stretches the spring L feet where L satisfies the equation
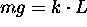 and k is the spring constant.
Since the equation (1) is normalized,
and k is the spring constant.
Since the equation (1) is normalized,
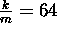 . Hence,
. Hence, 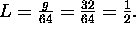
-
(8 points)
If
, the roots of the characteristic equation
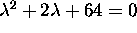 are
are
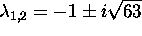 .
Hence,
.
Hence, 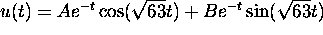 . The initial condition determines that
. The initial condition determines that
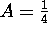 and
and 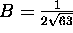 .
It follows that the position function is
.
It follows that the position function is
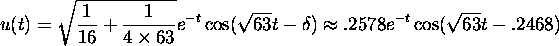
Above,
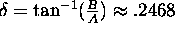 .
. - (6 points)
-
(3 points)
The points in time at which the mass returns to its equilibrium
are solutions of the equation u(t)=0. These must be solutions of
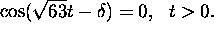 Hence,
Hence, 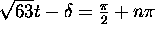 , where n is an integer.
The first time occurs when
, where n is an integer.
The first time occurs when 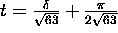 .
All times are given by
.
All times are given by
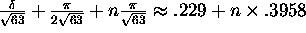 ,
where n is a non-negative integer.
,
where n is a non-negative integer. - (6 points)
The system returns to equilibrium infinitely many times
if
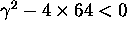 because in that case the characteristic equation
has two complex roots and the system vibrates.
The system never come back to its
equilibrium if the system is over-damped
because in that case the characteristic equation
has two complex roots and the system vibrates.
The system never come back to its
equilibrium if the system is over-damped 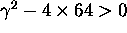 or
critically damped
or
critically damped 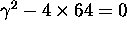 .
In other words, when
.
In other words, when 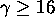 . To see that it suffices to check
the case
. To see that it suffices to check
the case 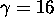 (since, if
(since, if 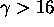 , the system will move even more
slowly having a larger damping force). When
, the system will move even more
slowly having a larger damping force). When 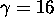 the solution to the initial value problem is
the solution to the initial value problem is
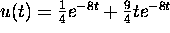 . We see that
u(t) is always positive for t;SPMgt;0.
Note: (the following was not required to get full credit)
If
. We see that
u(t) is always positive for t;SPMgt;0.
Note: (the following was not required to get full credit)
If 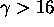 , the two roots
, the two roots 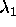 ,
, 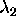 are negative.
Say
are negative.
Say  . Then
. Then
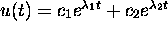 and the initial condition implies
that
and the initial condition implies
that 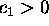 ,
,
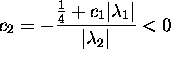 ,
and
,
and 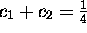 .
Hence,
.
Hence, 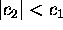 . It follows that
. It follows that
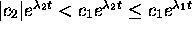 and u(t) is positive for all t;SPMgt;0.
and u(t) is positive for all t;SPMgt;0.
- (15 points)
The general solution of the equation
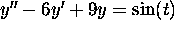 has the form
has the form 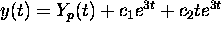 where
a particular solution
where
a particular solution 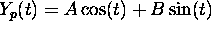 can be found
using the method of undetermined coefficients. Plugging in we get
the equation
can be found
using the method of undetermined coefficients. Plugging in we get
the equation
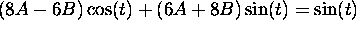 . Hence,
8A-6B=0 and 6A+8B=1 and
. Hence,
8A-6B=0 and 6A+8B=1 and
- (reduced to 5 points due to poor performance of entire class)
If u(0)=1, then
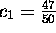 .
The behavior of y(t) in (2)
is dominated by the term
.
The behavior of y(t) in (2)
is dominated by the term 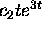 if
if 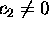 and by
the term
and by
the term 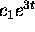 if
if 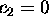 . Hence,
if
. Hence,
if 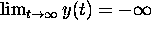 , then
, then 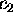 is negative.
The slope of the graph of the solution
at t=0 satisfies in that case the inequality:
is negative.
The slope of the graph of the solution
at t=0 satisfies in that case the inequality:
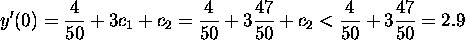
- (2 point)
We verify that
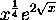 is
a solution of the differential equation
is
a solution of the differential equation
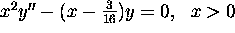 by plugging in. Indeed,
by plugging in. Indeed,
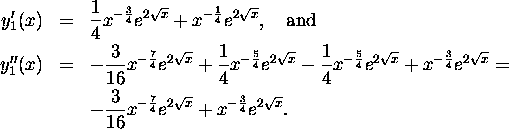
So,
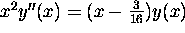 .
. - (13 points, a generous partial credit scheme)
We first find the general solution using the method of reduction of order.
Given one solution
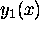 of a second order D.E. y''+p(x)y'+q(x)y=0
we look for a solution of the form
of a second order D.E. y''+p(x)y'+q(x)y=0
we look for a solution of the form 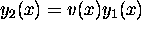 .
Then v(x) satisfies the differential equation
.
Then v(x) satisfies the differential equation
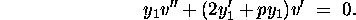
In our case, p(x)=0. So v(x) satisfies the differential equation
If we let u(x)=v'(x) and integrate both sides of (3) we get the equation
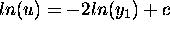 .
Hence,
.
Hence, 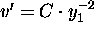 . We may choose C to be 1. Integrating once
more we get
. We may choose C to be 1. Integrating once
more we get
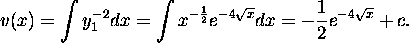
Hence,
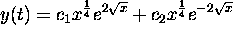 .
.
We can now find the particular solution satisfying the initial condition
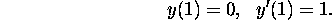
(It was not necessary to determine
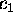 and
and 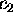 in order to get the full
credit). We get the equations
in order to get the full
credit). We get the equations
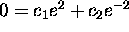 and
and 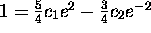 .
The solution is
.
The solution is