is linear.
Its normal form is 
.
The integrating factor is 
.
We then multiply by 
and integrate both sides
(using integration by parts on the right hand side):
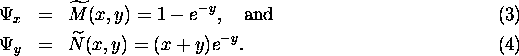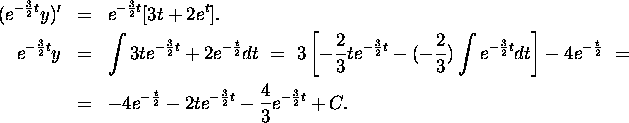
Thus, 
.
(b) (5 points)
The behavior of y(t) for large t is dominated by
the term 
if C=0 and by
the term 
if 
.
Hence, if 
,
then C ;SPMgt; 0.
The y-intercept is 
.
Thus, if C ;SPMgt; 0 then 
.
is equivalent to
Notice that it is linear in x. The tricky way to solve it would be
to find x as a function of y. Below we present the more straight-forward
method of finding an integrating factor making the equation exact.
Set N(x,y)=x+y and 
. Since 
and
are not equal, the equation is not exact.
Step I:
An integrating factor 
which is a
function of y can be found by solving the equation
. The equation is equivalent to
Integration of both sides and exponentiation shows that 
is a
solution of (2).
Step II: Set 
and
.
The equation
is an exact equation which is equivalent to
(1). Indeed 
.
We are looking for a solution defined implicitly by 
where
Integrating (3) we get that 
.
Equation (4) implies that 
. Integrating by
parts we find that
Hence the general solution is given by 
.
(b) (5 bonus points) The original equation has the form y'=f(x,y)
where 
is discontinuous along the line y=-x.
Both f and its partial 
are continuous away from this line in 
. Hence, by
the existence and uniqueness Theorem for first order O.D.E's (Theorem
2.4.1 in the text) a point 
with 
lies
on the graph of precisely one solution. If 
and 
then there is no solution through that point
because the slope y'=f would be infinite. As for the origin (0,0) we may
say that there is no solution because f is not defined at (0,0).
Note: A more precise answer (which was not required in order to get the 5 point
bonus) is that there is a unique differentiable solution of
(1) through the origin given implicitly by
choosing C=1. (Exercise: check that it is indeed differentiable!!!)
is homogeneous.
Using the substitution v=y/x (or y=vx) it is equivalent to
Assuming that 
(i.e., 
and 
, each of which is a
solution) we get the separable equation:
Integrating both sides (using partial fractions
) and
exponentiating we get
Substituting back v=y/x and simplifying we get that the general solution is:
Notice that the solution y=2x is obtained when C=0 but the solution
y=-2x is not obtained for any value of C. (It can be obtained as
the limit of solutions letting 
.)
has characteristic equation 
.
The two roots are 
and 
.
We get the two equations 
and 
.
The general solution is
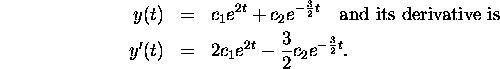
The initial condition translates to the two equations:
Solving for 
and 
we get the solution for the initial value problem
(b) (4 points) If 
,
then 
must be negative. Thus, the slope 
satisfies
are solutions of
the second order linear equation
by plugging each into the equation.
(b),(c) (4 points and 8 points) The solutions f and g are
twice-differentiable on
and the equation (5)
is linear. Hence, any linear combination with constant coefficients
is also a solution. In order to show that it is the general solution, we need to show that f and g are a fundamental set of solutions, i.e., that their Wronskian,
is not zero at some (and hence, by Abel's Theorem, at every)
point in . This is clearly the case.
(d) (3 points)
If y(x) is a twice differentiable solution on 
then on it must have the form 
(by part (c)). Hence, by continuity,
It follows that there does not exist any solution satisfying the initial
condition y(0)=1 and y'(0)=2.
Note: this does not contradict the Uniqueness and Existence Theorem
because if we normalize the equation to the form
y'' + p(x)y' + q(x)y = 0 we would get that 
and
are discontinuous at x=0.
describes the amount in a saving account with 
annual interest
compounded continuously.
In our case, in addition, we deposit continuously 2 thousands dollars per
year. We get the linear (and separable) first order differential equation:
(b) (10 points)
The general solution is 
. The initial condition
S(0)= 10 yields
Solve the equation 
to get
that 
. The person would have a million dollars at age
25+60.67=85.67 (Too late to enjoy it!).
Note:
It is realistic to expect an investment in the stock market to yield an
annual profit of 
. The same person would have a million dollars at age
.