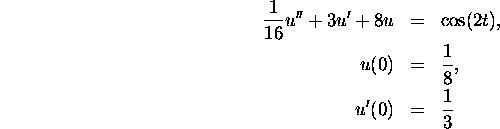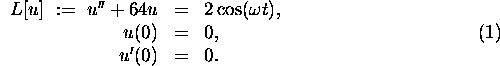Math 431 Solution of Midterm 2 Fall 1999
Answer:
The characteristic equation 
has roots
and 
.
Hence, the general solution has the form
where 
and 
are particular solutions of the non-homogenous
equations L[y]=2t+1 and 
.
We find these particular solutions of the form 
and
using the method of undetermined coefficients.
Plugging into the equation we get the equation
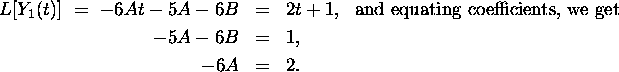
We conclude that 
.
Plugging into the equation we get
Hence, 
.
The general solution is
Answer: (Compare with homework problem 5 in Section 3.7)
The roots of the characteristic equation 
are 
.
Hence, 
and 
are a fundamental pair
of solutions. Their Wronskian is
The method of variation of parameters helps us find the solution to the initial value problem via the formula (using definite integration)
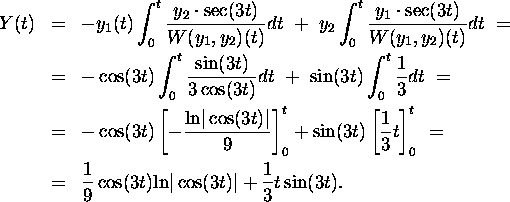
Another (longer) method would be to use indefinite integration in the
formula of variation of parameters to find a particular
solution Y(t). One then
determines the constants 
and 
for which
satisfies y(0)=0 and y'(0)=0.
You may use the fact that 
is a solution.
Answer: First method:
Most students found the general solution using the method of reduction of
order.
We are given that 
is a solution.
We look for a second solution of the form 
where v(t) satisfies the differential equation
Above, 
is the coefficient of y' in the
normalized equation.
Integrating both sides, we get
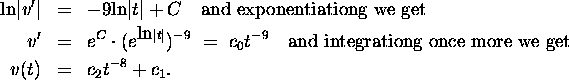
Hence, 
.
Second Method:
An easy way to find the general solution would be to realize
that the equation is an Euler equation
(see homework problems 38 and 39 in Section 3.4). We solve it by looking for a
solution of the form 
. Plugging into the equation we get
The two solutions of the equation 
are
and 
. Hence, the general solution is
a) (10 points) Find the solution of the system if the
frequency 
of the external force is 1.
Answer:
The solutions of the characteristic equation 
are 
and 
. The general solution has the form
and a particular solution 
can be found using the method of undetermined coefficient.
Plugging 
into the equation we get
and equating coefficients, we get 
and B=0 and the
general solution is
The initial condition determines that 
and 
.
The solution is thus
b) (3 points) What is the frequency
of the external force which will cause
the system to resonate (oscillate with increasing amplitude)?
Justify your answer!!!
Answer: The method of undetermined coefficients tells us that the equation (1) has a particular solution of the form
with s=0 if 
and s=1 if 
.
Hence,
resonance occurs when s=1, i.e., when the frequency of the
external force is equal to the frequency 8 of the homogeneous equation.
c) (4 points)
Find the solution of the resonating system when the frequency is
the one from part b.
Answer:
The equation
has a particular solution of the form
Differentiating twice, we get
Plugging Y(t) into the equation, we get
Thus 
and A=0 and
One checks that it satisfies the initial condition.
d) (3 points)
Carefully graph the solution of the resonating system in part c in the time
interval 
. Indicate all the t-axis intercepts.
where 
is a positive constant which depends on the damper.
a) (8 points) Solve the system if 
and 
,
u'(0)=0.
Answer:
The two roots of the characteristic equation 
are
The general solution is
The initial condition determines 
, 
,
and
b) (6 points) Graph your solution in part a. Determine the quasi-period and all points of time at which the mass passes through the equilibrium.
Answer: We first rewrite the solution (2) in the form
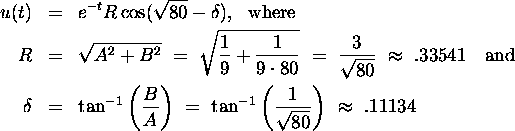
The quasi-period is 
.
The mass returns to its equilibrium when u(t)=0, i.e.,
when
Solving for t we get
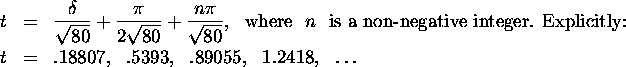
c) (6 points) Determine the range of values of for which
the position function u(t) is a decaying oscillation?
Justify your answer!!!
Answer: The position function u(t) is a decaying oscilation precisely when the roots of the characteristic equation are complex with a strictly negative real part. If the roots
are such, then the solution
is decaying (because 
) and oscilating (because 
).
This happens precisely when 
and
, i.e., when
stretches a spring 
.
The mass is acted upon by an external force of 
.
The mass is also attached to a damper with damping constant
.
Set up an initial value problem for the position u(t) of the mass
t seconds after it was pulled down (in the positive direction)
and set in motion downwards with an initial
velocity of 
. (Recall that the gravitational
constant g is ).
Do NOT solve the initial value problem!
Answer: The spring mass system satisfies the differential equation:
The information given translates to
We get that the mass is 
and the spring
constant is
.
The initial value problem is thus
