Math 431 Section 4 Final Exam Fall 1998

Show all your work. No credit will be given for a solution without an explanation. You may use a calculator. However, no credit will be given for a solution of a differential equation obtained using a symbolic differential equations software (e.g., on a TI-92).

1. Solve only four out of the following five differential equations (if no initial condition is specified, find the general solution).
   1. (12 points)

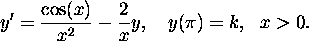
      Also determine the behavior of the solution as 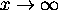if k=1. For which values of k will the solution be always positive?

   2. (12 points) .
   3. (12 points) .
   4. (12 points) .
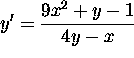   5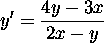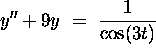. (12 points) .

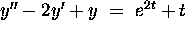   Solve only three out of the following four problems (2, 3, 4, 5):

2. (18 points)  
   1. Find the general solution of the system:

      

   2.   Find the solution satisfying the initial condition 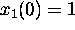and .
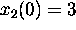   3.   Describe the behavior of the solution in part 2b as 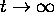(does its trajectory have any asymptotes?).
3.  
   1. (12 points)   Use the method of Laplace transform to solve the initial value problem (no credit will be given for a solution using another method).

      

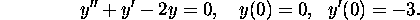
   2. (6 points) Express the solution of the given initial value problem in terms of a convolution integral: (use your solution to part (3a) to avoid repeating many of the computations)

      

4. (18 points)   Solve the initial value problem

   

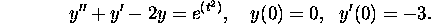
   where f(t) is defined by

   

   and is the Dirac delta ``function''. Hint: 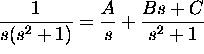for some choice of constants A, B, C.

5. (18 points)  
   1.   (3 points) A mass weighing 1.6 pounds stretches a spring 6.4 feet. Show that if the damping constant is then the spring mass system is governed by the equation

       

      where f(t) is the external force.

   2. (5 points)   In the following parts assume the statement of part 5a and work with the equation (1) even if you can not derive it. Solve the equation of motion of the system if there is no external force (f=0) and at time t=0 the spring is stretched 2 units below its equilibrium and the system is moving with velocity u'(0)=2 downwards (in the positive direction).
   3. (3 points)   Find all positive values of time at which the mass returns to equilibrium.
   4. (4 points)   Sketch the graph of the solution in part 5b. Explain its behavior as .
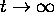   5. (3 points) Denote by 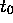the first time the mass returns to its equilibrium (calculated in part 5c). Find the magnitude c of the impulse 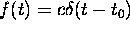needed to be applied at time 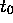in order to bring the system to rest. Explain!!!.

• About this document ...