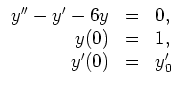
Answer:
The two roots of the
characteristic equation
![]() are
are ![]() and
and ![]() . Hence, the general solution is
. Hence, the general solution is
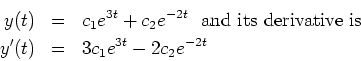
Plugging in ![]() , the initial value problem translates to the system of two
linear equations (where we regard
, the initial value problem translates to the system of two
linear equations (where we regard ![]() as a given constant and
as a given constant and ![]() and
and
![]() as the unknowns):
as the unknowns):
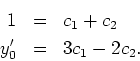
Solving for the coefficients, we get
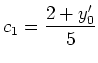 and
and
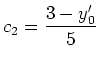 .
The solution is thus
.
The solution is thus
b) (5 points)
Find a condition on the slope ![]() which guarantees that
which guarantees that
![]() Explain your answer!
Explain your answer!
Answer: The limit
![]() is
is ![]() if and only if the coefficient
if and only if the coefficient
![]() is positive, i.e., if and only if
is positive, i.e., if and only if ![]() .
.
Use the direction field in order to sketch the graphs of the following two solutions.
- The solution satisfying
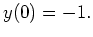
- The solution satisfying
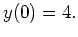
Answer:
We sketch the graph ![]() , of the solution
, of the solution ![]() satisfying
satisfying
![]() , by starting at the initial point
, by starting at the initial point
![]() and ``flowing'' along the direction field (in both
the negative and positive direction of
and ``flowing'' along the direction field (in both
the negative and positive direction of ![]() ).
The resulting solution is decreasing. We do the same for the solution through
).
The resulting solution is decreasing. We do the same for the solution through
![]() . The second solution is increasing.
. The second solution is increasing.
b) (4 points)
Based on the direction field, describe how the behavior of the solution,
as ![]() gets larger, depends on the value
gets larger, depends on the value ![]() in the initial condition
in the initial condition
Answer: The slope is zero along the curve ![]() and in
particular at
and in
particular at
![]() .
If
.
If ![]() , then the solution
, then the solution ![]() is increasing
and positive and its slope is increasing with
is increasing
and positive and its slope is increasing with ![]() .
Hence, the solution would satisfy
.
Hence, the solution would satisfy
![]() .
.
There is a range
![]() , for which the solution
is first decreasing, but eventually increasing. In part d we will see, that
this happens for
, for which the solution
is first decreasing, but eventually increasing. In part d we will see, that
this happens for ![]() . At this point, it is not obvious
what
. At this point, it is not obvious
what ![]() is (and even,
that it is a finite number and not
is (and even,
that it is a finite number and not ![]() ).
).
It seems plausible, that ![]() exists as a finite number
exists as a finite number ![]() ,
and solutions with
,
and solutions with
![]() are decreasing and satisfy
are decreasing and satisfy
![]() .
.
c) (13 points) Find the general solution of the differential equation (1).
Answer:
The equation is linear and its normal form is
with
Integrating both sides, we get the equations
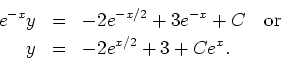
d) (2 points)
Solve the initial value problem (1) and
(2) (express your solution in terms of ![]() ).
).
Answer:
Plug ![]() for
for ![]() and
and ![]() for
for ![]() to get that
to get that ![]() and the solution is:
and the solution is:
e) (2 points)
Determine the range of values of ![]() for which the solution
for which the solution ![]() in part (d) satisfies
in part (d) satisfies
Factor out ![]() to write
to write
![]() .
We see, that
.
We see, that
![]() if and only if
if and only if
![]() .
.
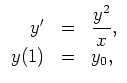 where
where
Answer:
If ![]() , then the solution is the constant function
, then the solution is the constant function ![]() .
The equation is separable. If
.
The equation is separable. If ![]() , then
we separate variables by dividing by
, then
we separate variables by dividing by ![]() to get:
to get:
Integrating both sides with respect to
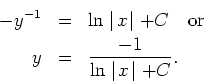
The initial condition determines
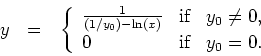
(b) (5 points)
Determine the largest interval, on which the solution of the initial
value problem is defined, in terms of the constant ![]() .
For which value of
.
For which value of ![]() , will the solution be defined for all
, will the solution be defined for all ![]() (as well as some other values of
(as well as some other values of ![]() )?
)?
Answer:
If ![]() , then the solution is not defined for
, then the solution is not defined for ![]() and
and ![]() .
Hence, the largest interval of definition, containing
.
Hence, the largest interval of definition, containing ![]() , is:
, is:
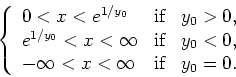
We see, that the solution is defined, for all
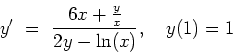
Answer:
The equation becomes exact, when written in the form
Set
Integrating both sides of equation (3), we get
for some function
Hence,
The initial condition determines, that
(b) (5 points)
Graph your solution in the window ![]() and
and
![]() .
.
Answer:
The solution of part a) was given by the quadratic equation
(5). The solutions for
a general quadratic equation ![]() are given by the formula
are given by the formula
![]() . Use the formula
with
. Use the formula
with ![]() ,
,
![]() and
and
![]() , to obtain
, to obtain
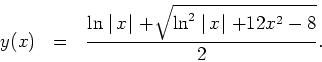
The sign in the numerator is determined by the initial condition