Math 235 Solution of Midterm 2 Spring 1999

1. (24 points) You are given below the matrix A together with its row reduced echelon form B

   

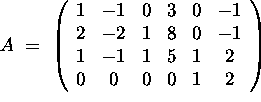
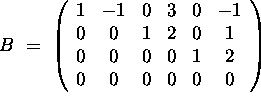
   a) (9 points) Find a basis for the null space Null(A) of A.

   Recall that Null(A) is the space of solutions of the linear system . Since A and B are row equivalent, Null(A)=Null(B). We have three free variables: , , and . Hence Null(B) is 3 dimensional. The equations

   

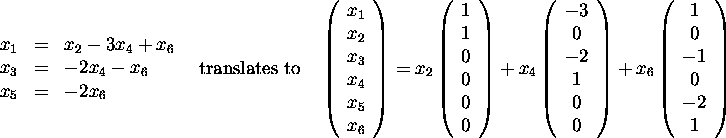
   and the three vectors 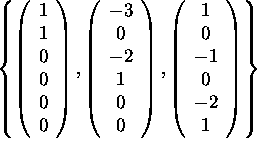are a basis of Null(A).

   b) (9 points) Find a basis for the column space of A.

   Take the pivot columns of A :

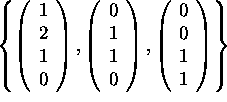
   c) (6 points) Is the vector 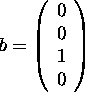in the column space of A? Justify your answer!

   No! The vector b is in Col(A) if and only if the system is consistent. We could check that it is inconsistent by row reduction of the augmented matrix. However, this would require a lot of work. Instead, use the fact that b is in Col(A) if and only if the vector b is a linear combination of the basis vectors in part (b). I.e., if and only if the augmented matrix 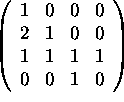does not have a pivot in the fourth column. But it does (Check by row reduction).

2. (10 points) Find a basis for the set of vectors in in the plane x+2y+z=0.

   Regard the equation of the plane as a linear ``system'' of one equation. So y and z are free variables and the general solution has the form

   

3. (24 points) Determine which of the following sets in is a subspace. If it is not, find a property in the definition of a subspace which this set violates. If it is a subspace, find a matrix A such that this set is either Null(A) or Col(A). Note: part (a), (b), (c) are analogous to Homework problems number 7, 9 ,10, 15 in section 4.2

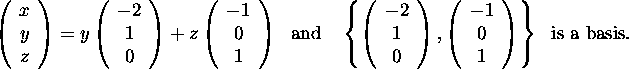
   (a) (9 points)

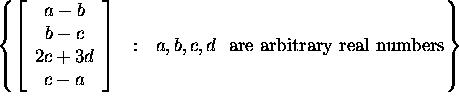
   This is a subspace.

   It is the set of vectors of the form 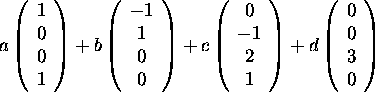Hence, it is the subspace spanned by these four vectors. Equivalently, it is the column space of the matrix having these 4 vectors as column vectors.

   (b) (9 points)

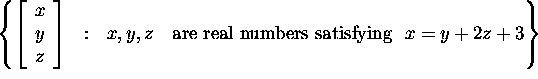
   This is not a subspace because the zero vector is not in this set (the equation is not homogeneous).

   (c) (6 points)

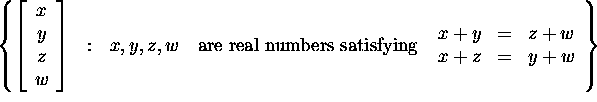
   This is a subspace. If we rewrite the equations in the form we get that this set is Null(A) where .

4. (16 points) a) (6 points) Compute the area of the parallelogram in with vertices
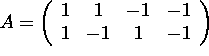   (1,1), (3,4), (6,2), (8,5). Caution: note that (0,0) is not a vertex.

   Translating by the vector (-1,-1) we get the parallelogram with vertices (0,0), (2,3), 5,1), (7,4) whose area is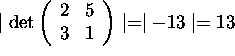

   b) (6 points) Compute the volume of the parallelepiped in with vertices

   , , , , , , , where

   

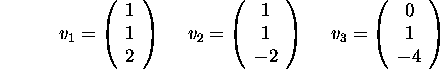
   The volume is the absolute value of the following determinants

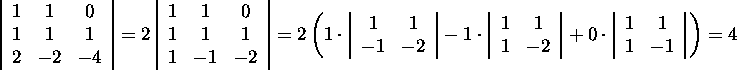
   c) (4 points) Use your answer in part (b) and the algebraic properties of determinants to compute the volume of the parallelepiped obtained if is replaced by
   where a, b, c are real numbers. (Express your answer in terms of a, b, c).

   By the algebraic properties of determinants we know that

   

   The first and second equalities follow from the fact that adding a multiple of one column to another does not change the determinant. The third equality reflects the property that if a matrix B is obtained from A by multiplication of a column by a scalar c then . The last equality is our computation in part (b). A more computational method is to express in terms of a, b, c

   

5. a) (4 points) Let A, B, and C be matrices satisfying the equation

   

   with A invertible. Solve for C in terms of A and B.

   Answer:

   b) (8 points) The inverse of 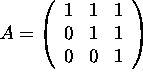is .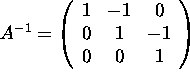

   c) (4 points) Compute the (2,2) entry of C in part (a) if A is given in part (b) and

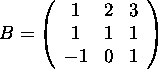
   . The second row of is (2, 1, 0). Multiplying by the second column of A we get .

6. (10 points) Let be the vector space of polynomials of degree . Recall that a vector in is a polynomial p(t) of the form where the coefficients are arbitrary real numbers.

   (a) (6 points) Show that the subset H of of polynomials p(t) of degree which in addition satisfy

   

   is a subspace of . (The straightforward answer would include the definition of a subspace and a verification that H satisfies all the properties.)

   Answer: A polynomial p(t) of the form is in H if and only if

    

   So H is the subset of of polynomials with the property that the sum of their coefficients is 0. To show that it is a subspace you can identify with by mapping the polynomial to the vector 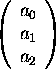and argue that (1) is the equation of a plane in through the origin. Alternatively, you can argue more abstractly using the definition of a subspace of a vector space:

   1) The zero polynomial is in H.

   2) If and are in H, then p+q is in H because (p+q)(1)=p(1)+q(1)=0+0=0.

   3) If p is a polynomial in H and c is a scalar then cp is in H because .

   (b) (4 points) Find a basis for H. Explain why the set you found is linearly independent and why it spans H.

   Answer: As a basis to the plane in given by equation (1) we can take the two vectors 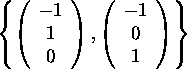(use the same method as in problem 2). Thus, the two polynomials

   

   are a basis for H.

• About this document ...