Math 235 Final Exam Spring 1999

1. (15 points) The matrices A and B below are row equivalent (you do not need to check this fact).

   

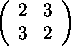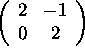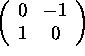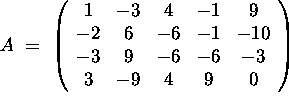
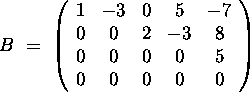
   a) What is the rank of A?

   b) Find a basis for the null space Null(A) of A.

   c) Find a basis for the column space of A.

   d) Find a basis for the row space of A.

2. (4 points) The null space of the matrix A is 2 dimensional. What is the dimension of (a) the Row space of A? (b) the Column space of A? Justify your answer!
3. (15 points)
   1. Show that the characteristic polynomial of the matrix 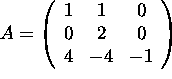is .
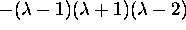   2. Find a basis of 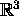consisting of eigenvectors of A.
   3. Find an invertible matrix P and a diagonal matrix D such that the matrix A above satisfies

      

4. (12 points) Determine for which of the following matrices A below there exists an invertible matrix P (with real entries) such that is a diagonal matrix. You do not need to find P. Justify your answer!
   1. 
   2. 
   3. 
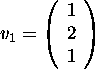5. (22 points) Let W be the plane in spanned by and
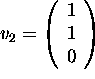
   Note: Parts 1, 2, 3 are mutually independent and are not needed for doing parts 4, 5, 6.
   1.   Find the length of .
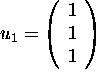   2.   Find the distance between the two points and in .
   3.   Find a vector of length 1 which is orthogonal to W.
   4.   Find the projection of to the line spanned by .
   5.   Write as the sum of a vector parallel to and a vector orthogonal to .
   6.   Find an orthogonal basis for W.

6. (16 points) Let W be the plane in spanned by and
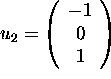
   1. Find the projection of 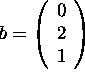to W.
   2. Find the distance from b to W.
   3. Find a least square solution to the equation Ax=b where A is the 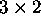matrix with columns 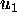and 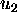. I.e., find a vector x in 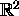which minimizes the length .
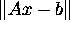   4. Find the coefficients 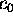, 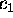of the line 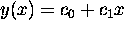which best fits the three points 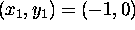, , 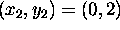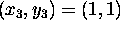in the x,y plane. The line should minimize the sum 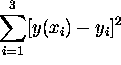. Justify your answer!

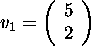7. (16 points) The vectors and 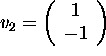are eigenvectors of the matrix .
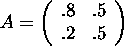   1. The eigenvalue of 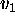is ______
      

      The eigenvalue of 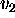is _______
      

   2. Find the coordinates of 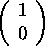in the basis .
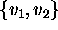   3. Compute .
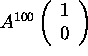   4. As n gets larger, the vector 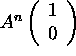approaches _____. Justify your answer.

• About this document ...