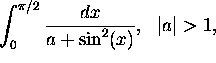
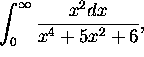
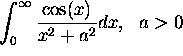next up previous
Next: About this document

Math 621 Homework Assignment 8 Spring 2000

Due: Monday, May 15

  1. Compute the following integrals:
    1. tex2html_wrap_inline148
    2. tex2html_wrap_inline150
    3. tex2html_wrap_inline152 real,
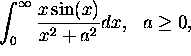    4. tex2html_wrap_inline154 real,
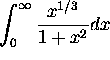
    5. tex2html_wrap_inline156
    1. Find a function 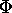tex2html_wrap_inline158 , harmonic on the domain 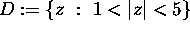tex2html_wrap_inline160 and with the following boundary values:

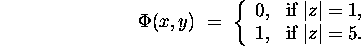
      displaymath138

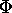    2. Find the level curves of tex2html_wrap_inline158 .
  3.   Ahlfors, page 171 Problem 4: Let tex2html_wrap_inline164 , tex2html_wrap_inline166 be complementary arcs on the unit circle. Set U=1 on tex2html_wrap_inline164 and U=0 on tex2html_wrap_inline166 .
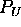    1. Find explicitly a harmonic function tex2html_wrap_inline176 in the open unit disk satisfying

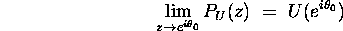
      displaymath139

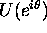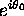      provided tex2html_wrap_inline178 is continuous at tex2html_wrap_inline180 .

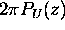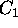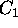    2. Show that tex2html_wrap_inline182 equals the length of the arc, opposite tex2html_wrap_inline164 , cut off by the straight lines through z and the end points of tex2html_wrap_inline164 .
    1. Basic Exam, August 97 Problem 9: Find a function u, harmonic in the unit disk, continuous on 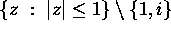tex2html_wrap_inline192 , and satisfying

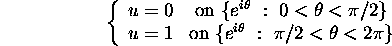
      displaymath140

    2. Find the level curves of u.
    3. Find a harmonic conjugate v of u.
    4. How are the level sets of u and v related?
    1. Solve the boundary value problem

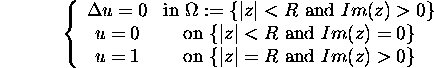
      displaymath141

      in two ways:

      1. By using a conformal map from tex2html_wrap_inline204 onto the first quadrant of the complex plane.
      2. By using the Reflection Principle (Lang Theorems 1.1 and 1.2 page 294) and your solution to Problem 3.
    2. Find the level sets of u.
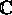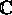    1. Basic Exam September 98 Problem 9b: Prove that the image of the complex plane tex2html_wrap_inline208 , under a non-constant entire function, is dense in tex2html_wrap_inline208 .
    2. Prove that there does not exist a one-to-one conformal map from the complex plane 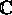tex2html_wrap_inline208 onto the unit disk.
  7. Lang page 307 Problem 7: The holomorphic automorphism group of a simply connected open set U acts transitively on points. More precisely, let tex2html_wrap_inline216 be a simply connected open set, tex2html_wrap_inline218 , tex2html_wrap_inline220 two points in U. Use the Riemann-Mapping-Theorem (Lang, page 306) to prove that there exists a holomorphic automorphism f of U such that tex2html_wrap_inline228 . Distinguish the cases when tex2html_wrap_inline230 and tex2html_wrap_inline232 .
  8. Basic Exam, January 99 Problem 7: Find a one-to-one conformal map from the region obtained as the intersection of the two unit disks:

    displaymath142

    onto the upper half plane. Hint: show that the angle between the two circles, at each of the two points of intersection, is tex2html_wrap_inline234 . For the smoothing of the boundary, observe that the function tex2html_wrap_inline236 , tex2html_wrap_inline238 , is well defined on the region tex2html_wrap_inline240 (why?) and maps tex2html_wrap_inline204 onto the upper half plane.


next up previous
Next: About this document

Eyal Markman
Tue May 23 11:22:58 EDT 2000