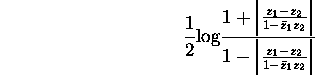-
Lang, page 171 Problem 10: Show that any function, which is meromorphic on
the extended complex plane, is a rational function.
(You may use Problem 7 in Homework assignment 4).
-
Lang, page 171 Problem 11:
Define the order
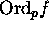 of a meromorphic function f at a point p
to be
of a meromorphic function f at a point p
to be
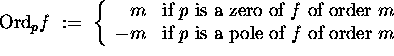
Above, m could be zero, meaning that f is analytic at p and 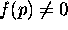 .
.
Let f be a meromorphic function on the extended complex plane 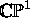 (so a rational function by problem
1).
(so a rational function by problem
1).
-
Prove that
In other words, the number of points in the fiber
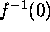 , counted with multiplicity, is equal to the number of points
in
, counted with multiplicity, is equal to the number of points
in 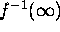 , counted with multiplicity.
, counted with multiplicity.
-
Prove that all fibers
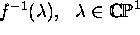 , of f
consist of the same number of points, provided they are
counted with multiplicity,
, of f
consist of the same number of points, provided they are
counted with multiplicity,
-
Ahlfors, page 130 Problem 5:
Let
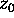 be an isolated singularity of an analytic function f.
Prove that if
be an isolated singularity of an analytic function f.
Prove that if 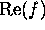 is bounded from above or below,
then
is bounded from above or below,
then 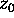 is a removable singularity.
Ahlfors' Hint: Apply a linear l.f.t.
Note: Personally, I find it easier to avoid using a l.f.t
(which does not seem to help rule-out the case of a pole). Instead, a short
proof can be obtained using both the Casorati-Weirstrass and the Open Mapping
Theorems.
is a removable singularity.
Ahlfors' Hint: Apply a linear l.f.t.
Note: Personally, I find it easier to avoid using a l.f.t
(which does not seem to help rule-out the case of a pole). Instead, a short
proof can be obtained using both the Casorati-Weirstrass and the Open Mapping
Theorems. -
Let
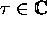 be a complex number and assume that
be a complex number and assume that
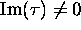 .
A function f is said to be
doubly periodic with periods 1 and
.
A function f is said to be
doubly periodic with periods 1 and 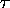 if
if
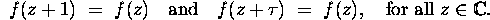
Show that every entire function,
which is doubly periodic with periods 1 and 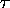 , is necessarily constant.
(We will see that there exist non-constant, doubly periodic, meromorphic
functions
, is necessarily constant.
(We will see that there exist non-constant, doubly periodic, meromorphic
functions  ).
).
-
Jan 96 Basic Exam, Problem 5:
Find the maximum value of the function
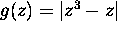 on the disk
on the disk
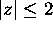 . Justify your answer!
. Justify your answer! -
Lang page 213 Problem 1: Let f be analytic on the unit disc D,
and assume that
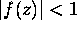 on the disc.
Prove that if there exist two distinct points
a, b in the disc, which are fixed under f
(that is f(a)=a and f(b)=b), then f(z)=z.
on the disc.
Prove that if there exist two distinct points
a, b in the disc, which are fixed under f
(that is f(a)=a and f(b)=b), then f(z)=z. -
Lang, page 219 problem 8:
Use Schwarz's Lemma to prove that
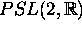 is the group of
holomorphic automorphisms of the upper half plane.
(
is the group of
holomorphic automorphisms of the upper half plane.
( 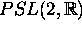 is naturally identified with the group of fractional
linear transformations which are associated to invertible
is naturally identified with the group of fractional
linear transformations which are associated to invertible
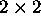 matrices with real coefficients and determinant 1).
Hint: You may use the fact (proven in class when we showed that l.f.t
preserve the notion of symmetry with respect to lines and circles)
that, if a l.f.t. f(z) takes
matrices with real coefficients and determinant 1).
Hint: You may use the fact (proven in class when we showed that l.f.t
preserve the notion of symmetry with respect to lines and circles)
that, if a l.f.t. f(z) takes 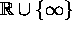 to itself, then
it can be written in the form
to itself, then
it can be written in the form 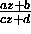 , with real coefficients
a, b, c, d.
, with real coefficients
a, b, c, d. -
Lang page 213 Problem 2:
Let
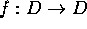 be a holomorphic map from the disc into itself.
Prove that, for all
be a holomorphic map from the disc into itself.
Prove that, for all 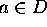 , we have
, we have
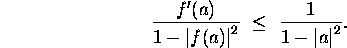
Moreover, equality for some a implies that f is a linear fractional
transformation.
Hint: Let g be an automorphism of D such that g(0)=a,
and let h be the automorphism which maps f(a) on 0.
Let 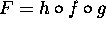 . Compute F'(0) and apply the Schwarz Lemma.
. Compute F'(0) and apply the Schwarz Lemma.
-
Ahlfors, page 136 Problem 2:
Let f(z) be analytic and
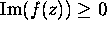 for all z in the upper half plane. Show that
for all z in the upper half plane. Show that
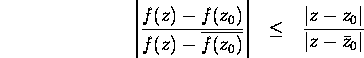
and, writing z=x+iy,

Moreover, equality, in either one of the two inequalities above,
implies that f is a linear fractional
transformation.
-
Ahlfors, page 136 Problem 6:
If
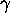 is a path, piecewise of type
is a path, piecewise of type 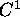 ,
contained in the open unit disc D, then the integral
,
contained in the open unit disc D, then the integral

is called the non-euclidean length or hyperbolic length
of 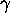 . Let
. Let 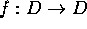 be an analytic function from the
disc into itself.
Show that f maps every
be an analytic function from the
disc into itself.
Show that f maps every 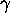 on a path with smaller or equal
non-euclidean length.
Deduce that a linear fractional transformation from D onto itself
preserves non-euclidean lengths.
on a path with smaller or equal
non-euclidean length.
Deduce that a linear fractional transformation from D onto itself
preserves non-euclidean lengths.
-
Ahlfors, page 136 Problem 7: (Modified)
It can be shown, that the path of smallest non-euclidean length,
joining the origin 0 to a point
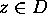 , is the straight line segment
between them.
, is the straight line segment
between them.
-
Use this fact to show that the path of smallest non-euclidean length,
that joins two given points in the unit disk, is the piece of the circle C
which is orthogonal to the unit circle
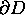 .
The shortest non-euclidean length is called the
non-euclidean distance.
.
The shortest non-euclidean length is called the
non-euclidean distance. -
Show that the non-euclidean distance between
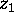 and
and 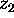 is
is
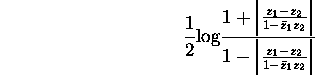
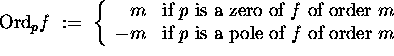
![]() .
.
![]() (so a rational function by problem
1).
(so a rational function by problem
1).
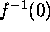 , counted with multiplicity, is equal to the number of points
in
, counted with multiplicity, is equal to the number of points
in 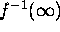 , counted with multiplicity.
, counted with multiplicity.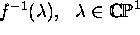 , of f
consist of the same number of points, provided they are
counted with multiplicity,
, of f
consist of the same number of points, provided they are
counted with multiplicity,
![]()
![]() , is necessarily constant.
(We will see that there exist non-constant, doubly periodic, meromorphic
functions
, is necessarily constant.
(We will see that there exist non-constant, doubly periodic, meromorphic
functions ![]() ).
).![]()
![]() . Compute F'(0) and apply the Schwarz Lemma.
. Compute F'(0) and apply the Schwarz Lemma.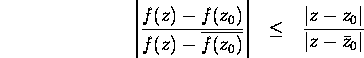
![]()
![]()
![]() . Let
. Let ![]() be an analytic function from the
disc into itself.
Show that f maps every
be an analytic function from the
disc into itself.
Show that f maps every ![]() on a path with smaller or equal
non-euclidean length.
Deduce that a linear fractional transformation from D onto itself
preserves non-euclidean lengths.
on a path with smaller or equal
non-euclidean length.
Deduce that a linear fractional transformation from D onto itself
preserves non-euclidean lengths.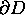 .
The shortest non-euclidean length is called the
non-euclidean distance.
.
The shortest non-euclidean length is called the
non-euclidean distance.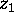 and
and 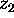 is
is