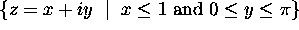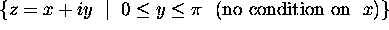Math 621 Homework Assignment 1 Spring 2000

Due: Thursday, February 10

1. Lang, Ch. 1 Section 2 page 11: 7, 10, 11, 12, 13
2. Lang, Ch. 1 Section 3 page 17 problem 4: Let . Describe the image under f of the following sets:
   1. .
   2. .
3. Lang, Ch. 1 Section 4 page 26 problem 3: Show that for any complex number , we have

   

   If , show that

   

4. Let u, v be real valued functions defined on an open set U in . Prove that if u and v have continuous partial derivatives, then the function

   

   is differentiable throughout U in the sense that

   

   Hint: Bound the quotient by a sum of two terms each depending only on u or v, define and , , and use the Mean Value Theorem for a(t) and b(t).

5. Ahlfors, Ch. 1 Section 2.1 page 15 problem 2: Prove that the points , , are vertices of an equilateral triangle if and only if

   

6. 1. Show that if 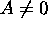, the set of points

      

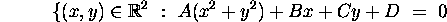
      is either empty or a circle. Determine the center and the radius. What happens when A=0?

   2. Show that the set of points

      

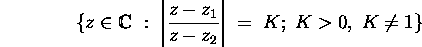
      is a circle. Determine the center and the Radius. What happens when K=1?

7. Let , , be a polynomial of degree d. Show that there exist positive constants k, K, and R such that

   

8. Let with . Show that the roots of P(z)=0 satisfy . (Hint: Obtain a lower bound for for ).
9. Given a complex valued function f of one complex variable z, define

   

   Assume f is holomorphic.

   1.   Show that , , , and .
   2.   Show that .
   3. Use parts 9a and 9b to show that is HARMONIC provided .

• About this document ...