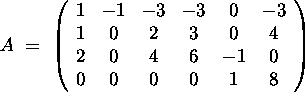
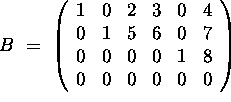
a) (10 points) Find a spanning set for (i.e., a set of vectors which spans) the null space Null(A) of A.
Answer:
We use the row reduced echelon form to write, in parametric form,
the general solution of ![]() (i.e., the general vector in Null(A)).
The free variables are:
(i.e., the general vector in Null(A)).
The free variables are: ![]() ,
, ![]() , and
, and ![]() .
Hence, the general solution is
.
Hence, the general solution is
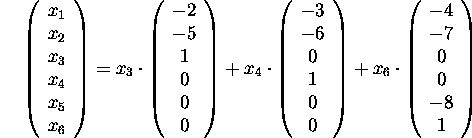
and the three column vectors above span Null(A).
b) (8 points) Are the column spaces ![]() and
and ![]() equal? Justify your answer carefully!
(either explain why they are equal, or
find a vector in one that does not belong to the other).
equal? Justify your answer carefully!
(either explain why they are equal, or
find a vector in one that does not belong to the other).
Answer: No, the two column spaces are different! For example, the last column of A has a non-zero fourth entry, while any vector in Col(B) is a linear combination of the columns of B, and hence, its fourth entry is zero.
 be the
be the 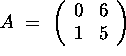 .
.
a) (5 points) Show that the matrix A-5I is invertible.
Note that A-5I is simply
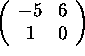 .
.
Answer
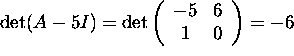 . Since
. Since ![]() , the matrix A-5I is invertible.
, the matrix A-5I is invertible.
b) (5 points) Express the determinant of the ![]() matrix A-tI in terms of the
scalar parameter t.
matrix A-tI in terms of the
scalar parameter t.
Answer
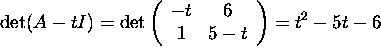 .
.
c) (6 points) Show that there are precisely two values of t for which the matrix A-tI is not invertible. Find these values of t.
Answer
A-tI is not invertible if and only if
its determinant vanishes.
We find those values of t buy solving the quadratic equation
![]() . The two solutions are t=6 and t=-1.
. The two solutions are t=6 and t=-1.
-
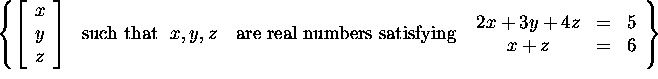
Answer This subset of
 does not contain the zero vector.
Hence, it is not a subspace.
does not contain the zero vector.
Hence, it is not a subspace. -
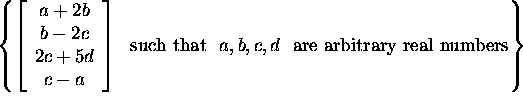
Answer
We can write the general element as a linear combination
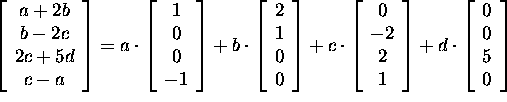 Hence, this subset is a subspace, which is equal to the
column space of the matrix
Hence, this subset is a subspace, which is equal to the
column space of the matrix
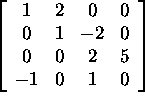
-

Answer:
This subset of ![]() is the general solution of the system
of homogeneous linear equations
is the general solution of the system
of homogeneous linear equations
![]() It is hence a subspace which is equal to the Null space of
It is hence a subspace which is equal to the Null space of
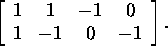
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() where
where
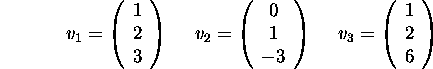
Answer:
The volume is the absolute value of the determinant of the ![]() matrix M with columns
matrix M with columns ![]() and
and ![]() .
.
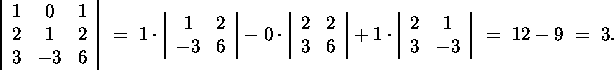
b) (8 points) Let T be the linear transformation from ![]() to
to
![]() sending a vector
sending a vector ![]() to
to ![]() , where
A is the matrix
, where
A is the matrix
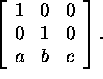 Compute the volume of the
parallelepiped obtained as the image of the one in part (a)
under the transformation T.
Express your answer in terms of a, b and c.
Note: The image is the parallelepiped with vertices
Compute the volume of the
parallelepiped obtained as the image of the one in part (a)
under the transformation T.
Express your answer in terms of a, b and c.
Note: The image is the parallelepiped with vertices
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
Answer:
First Method:
![]() where M is the matrix in part (a).
where M is the matrix in part (a).
Second Method: Calculate directly the determinant.
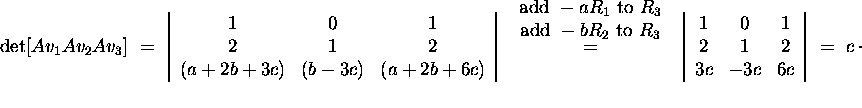 .
Hence the volume is 3|c|.
.
Hence the volume is 3|c|.
![]()
with A invertible. Solve for C in terms of A and B.
Answer: Multiply both sides by ![]() on the left to get
on the left to get
![]() . Then multiply both sides by A on the right
to get
. Then multiply both sides by A on the right
to get ![]() .
.
b) (10 points) Let 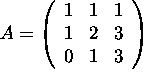 Compute its inverse
Compute its inverse ![]() . (Check that
. (Check that ![]() .)
.)
Answer: Augment A by the ![]() identity matrix and row reduce:
identity matrix and row reduce:
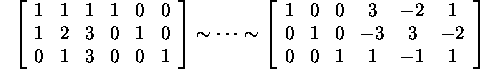
Hence, 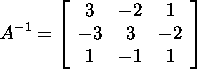
c) (6 points)
Compute the (2,3) entry of ![]() if A is given in part (b) and
if A is given in part (b) and
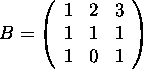
Answer: Calculate the product of the second row of A times B. Then
take the product of the resulting row vector with the third column of
![]() .
.
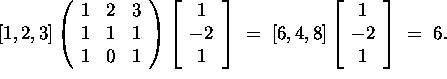
a) (6 points)
Show that the subset H of ![]() of polynomials p(t) of degree
of polynomials p(t) of degree ![]() which in addition satisfy
which in addition satisfy
is a subspace of ![]() . (The straightforward answer would include the
definition of a subspace and a verification that H satisfies
all the properties.)
. (The straightforward answer would include the
definition of a subspace and a verification that H satisfies
all the properties.)
Answer:
We check the three conditions for a subset of the vector space
![]() to be a subspace:
to be a subspace:
i) The zero vector ![]() has value 0 when t=0 and when t=1.
Hence, the zero vector is in H.
has value 0 when t=0 and when t=1.
Hence, the zero vector is in H.
ii) (H is closed under addition) If p and q are in H, then they satisfy equation (1). Consequently, p(0)=0, p(1)=0, q(0)=0, and q(1)=0. We need to check that their sum satisfied equation (1) as well. Indeed:
(p+q)(0)=p(0)+q(0)=0+0=0 and (p+q)(1)=p(1)+q(1)=0+0=0.
iii) (H is closed under scalar multiplication) We need to check that if p is in H and c is a scalar, then cp satisfy equation (1) as well. Indeed:
![]() and
and
![]() .
.
b) (4 points) Find a spanning set for H. Explain why the set you found spans H.
Answer: We can rewrite equation (1) explicitly in the form
![]()
We find the general solution,
regarding ![]() ,
, ![]() and
and ![]() as unknowns:
as unknowns:
![]() is free and
is free and
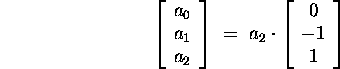
If we choose ![]() , we get the polynomial
, we get the polynomial ![]() .
Any other polynomial in H is a scalar multiple of this one.
Hence,
.
Any other polynomial in H is a scalar multiple of this one.
Hence,
![]()