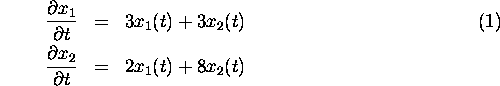
The system of two equations
is an example of a linear system of ordinary differential equations
(because it involved derivatives).
A solution of (1) is a pair of two differentiable functions
![]() and
and ![]() which satisfy the two equations.
You can think about the system geometrically:
which satisfy the two equations.
You can think about the system geometrically:
Suppose that the ![]() ,
, ![]() plane is the surface of the sea, and the
velocity vector of the water at any point
plane is the surface of the sea, and the
velocity vector of the water at any point
![]() is
is
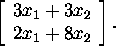 A solution
A solution
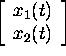 is a parametrized curve in
is a parametrized curve in ![]() indicating the path of a raft
floating on the surface of the sea. The system (1) reads:
indicating the path of a raft
floating on the surface of the sea. The system (1) reads:
If the solution passes through the point with coordinates
![]() at time t, then its velocity vector at that time is equal to the velocity
vector of the water at that point.
at time t, then its velocity vector at that time is equal to the velocity
vector of the water at that point.
The system of equations can be written in matrix form: (where x' stands for
![]() )
)
A pair of functions ![]() and
and ![]() is a solution of (1)
if and only if the vector valued function
is a solution of (1)
if and only if the vector valued function
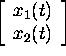 is a solution of (2).
is a solution of (2).
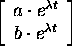 is a solution of the equation
is a solution of the equation
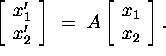
Hint: Simply plug
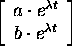 for
for
![]() on both sides of the equation. Recall the Chain Rule:
on both sides of the equation. Recall the Chain Rule:
![]()
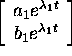 and
and
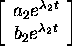 are solutions of (2).
are solutions of (2).
It is easy to check that the sum of two (vector valued) solutions of (2) is again a solution of (2). Conclude that
is a solution for any choice of
constants ![]() and
and ![]() .
.