-
Find the value of the integral
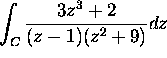 for:
for:
(a) C the circle 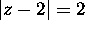 .
.
(b) C the circle 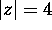 .
.
-
Suppose that
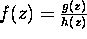 ,
, 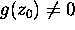 and h(z) has a zero
of
order 2 at
and h(z) has a zero
of
order 2 at 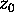 . Prove that
. Prove that
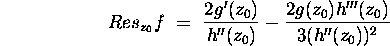
-
Compute the integral of the following functions over the circle
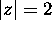 :
:
(a) 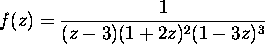
(b) 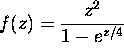
(c) 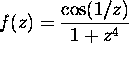
-
Let P(z) and Q(z) be polynomials and suppose that
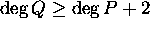 . Show that
. Show that
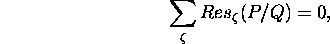
where the sum runs over all singularities of the rational function P/Q.
Do this problem in two ways: (1) Directly, without considering the residue at
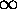 . (2) As a special case of problem
6.
. (2) As a special case of problem
6.
-
Lang Problem 37 page 190:
Let f be analytic on
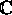 with exception of a finite number of
isolated singularities
with exception of a finite number of
isolated singularities 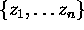 . Define the residue at
infinity
. Define the residue at
infinity
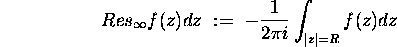
for 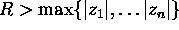 .
.
(a) Show that 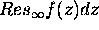 is independent of R.
is independent of R.
(b) Show that the sum of the residues of f in the extended complex plane
 is equal to zero.
(This result is often refered to as The residue Theorem.)
is equal to zero.
(This result is often refered to as The residue Theorem.)
-
Lang Problem 38 page 190 (Cauchy's Residue Formula on the Riemann Sphere).
-
Basic Exam, September 1998 Problem 5:
Compute
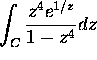 where
C denotes the circle
where
C denotes the circle 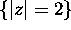 transversed counterclockwise.
Hint: Use the residue at infinity
(problem 6) to save
computations.
transversed counterclockwise.
Hint: Use the residue at infinity
(problem 6) to save
computations. -
Basic Exam, January 2000 Problem 7:
Let f be a one-to-one holomorphic map from a region
 onto a
region
onto a
region  . Suppose that
. Suppose that 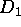 contains the closure of the disk
contains the closure of the disk
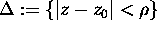 . Prove that for
. Prove that for 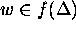 the inverse function
the inverse function 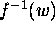 is given by
is given by
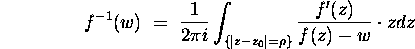
-
Let P(z) be a polynomial of degree d and
assume that the roots
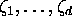 of P
are simple. Show that for R sufficiently large:
of P
are simple. Show that for R sufficiently large:
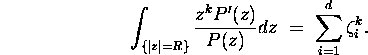
-
Lang page 189 Problem 29:
Let U be a connected open set, and let D be an open disk whose closure
is contained in U.
Let f be analytic on U and not constant. Assume that the absolute
value
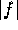 is constant on the boundary of D.
Prove that f has at least one zero in D.
Hint:
Consider
is constant on the boundary of D.
Prove that f has at least one zero in D.
Hint:
Consider 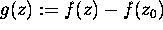 with
with 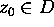 .
.
-
Basic Exam January 2000 Problem 9:
Prove that the equation

has 3 roots in the unit disk 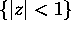 .
.
-
Basic Exam, August 99 Problem 4:
Let
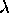 be a real number larger that 1. Show that the equation
be a real number larger that 1. Show that the equation
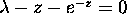 has exactly one solution in the half plane
has exactly one solution in the half plane
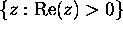 . Moreover, the solution is real.
. Moreover, the solution is real. -
Basic Exam, January 99 problem 3:
- (a)
- Determine the number of zeroes of
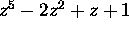 in the
disk
in the
disk 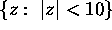 .
.
- (b)
-
Compute the integral
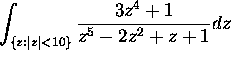 .
.
-
(Recommended Problem, you need not handed it in)
Lang Page 191 Problem 40 (modified):
Let a,
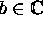 with
with 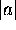 and
and 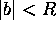 . Let
. Let 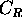 be
the circle of radius R.
be
the circle of radius R.
a) Show that there is an analytic branch of 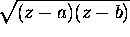 defined in
defined in 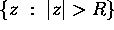 and such that
is analytic with value 1 at
and such that
is analytic with value 1 at 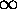 .
.
b) Evaluate
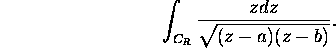
c) Evaluate
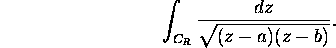
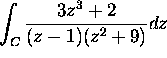 for:
for:
![]() .
.
![]() .
.![]()
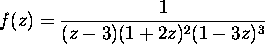
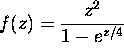
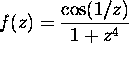
![]()
![]() . (2) As a special case of problem
6.
. (2) As a special case of problem
6.![]()
![]() .
.
![]() is independent of R.
is independent of R.
![]() is equal to zero.
(This result is often refered to as The residue Theorem.)
is equal to zero.
(This result is often refered to as The residue Theorem.)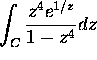 where
C denotes the circle
where
C denotes the circle ![]()
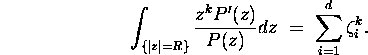
![]()
![]() .
.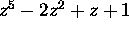 in the
disk
in the
disk 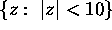 .
.
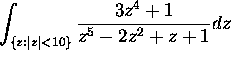 .
.
![]() defined in
defined in ![]() and such that
is analytic with value 1 at
and such that
is analytic with value 1 at ![]() .
.
![]()
![]()