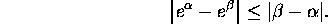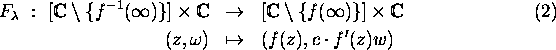Next: About this document
Math 621 Homework Assignment 3
Spring 2000
Due: Tuesday, March 7
Problems 3, 7, 8, 10, 12 are recommended, but you need not hand them in.
-
-
Find a function H(x,y) harmonic in the domain
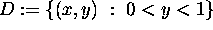 and such that
and such that  on the line
on the line 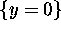 and
and 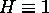 on the line y=1.
on the line y=1. -
Find a function G(x,y) harmonic in the region inside the circle
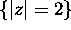 and outside the circle
and outside the circle 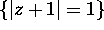 and such that
and such that
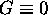 on the inner circle and
on the inner circle and 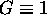 on the outer circle.
Hint: See HW 2 problem 2(a).
on the outer circle.
Hint: See HW 2 problem 2(a).
-
Lang page 238-239 problems 12 part c (interpret the result geometrically),
14 parts b,c, 13 part c (classify the fixed points according to Problem 14).
-
Let C and C' be circles in the complex plane. Let
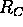 and
and 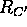 be the corresponding reflections (sending a point z to the symmetric point
be the corresponding reflections (sending a point z to the symmetric point
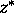 ).
Show that if T is a fractional linear transformation, then
).
Show that if T is a fractional linear transformation, then
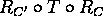 is a fractional linear transformation.
is a fractional linear transformation. -
Ahlfors page 83 problem 2: Reflect the imaginary axis, the line x=y, and the circle
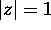 in the circle
in the circle 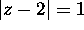 .
. -
Ahlfors page 83 problem 4: Find the linear fractional transformation which
carries the circle
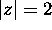 into
into 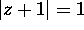 , the point -2 into the
origin, and the origin into i.
, the point -2 into the
origin, and the origin into i. -
Ahlfors page 83 problem 5: Find the most general linear fractional
transformation of the circle
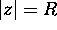 into itself.
into itself. -
Ahlfors page 83 problem 6:
Suppose that a linear transformation carries a pair of concentric circles into
another pair of concentric circles.
Prove that the ratio of the radii must be the same.
-
Ahlfors page 83 problem 7:
Find a l.f.t which carries
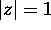 and
and 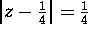 into concentric circles. What is the ratio of the radii?
into concentric circles. What is the ratio of the radii? -
Ahlfors page 33 problem 4:
What is the general form of a rational function (of arbitrary degree)
which has absolute value 1 on the circle
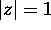 ? In particular, how are the zeros and poles related to each other? (You may use the
Fundamental Theorem of Algebra stated in Corollary 7.6 page 130 in Lang.
We will prove it later in the course).
Hint: Prove first that the rational function f satisfies
? In particular, how are the zeros and poles related to each other? (You may use the
Fundamental Theorem of Algebra stated in Corollary 7.6 page 130 in Lang.
We will prove it later in the course).
Hint: Prove first that the rational function f satisfies
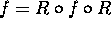 , where R is the reflection with respect to the unit
circle.
, where R is the reflection with respect to the unit
circle. -
Ahlfors page 33 problem 5:
If a rational function is real on
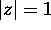 , how are the zeros and poles
situated?
, how are the zeros and poles
situated? -
Let
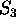 be the permutation group of the set
be the permutation group of the set 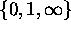 .
For each permutation
.
For each permutation 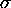 , denote by
, denote by 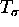 the fractional linear
transformation taking
the fractional linear
transformation taking 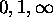 to
to 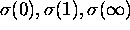 .
.
-
Find the six l.f.t
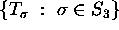 .
. -
The orbit of
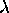 is the set
is the set
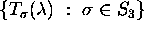 .
Show that all but two
.
Show that all but two 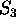 orbits in
orbits in
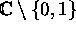 consist of six elements.
One special
consist of six elements.
One special 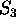 orbit in
orbit in
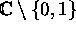 consists of two elements and
the other special orbit consists of three elements.
consists of two elements and
the other special orbit consists of three elements.
-
We have seen that the cross ratios
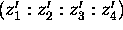 and
and 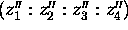 are equal, if and only if there exists a
linear fractional transformation mapping the first ordered 4-tuple to
the second. We work out the analogous statement for unordered
sets of 4 distinct points.
Let j be the rational function (of degree 6)
are equal, if and only if there exists a
linear fractional transformation mapping the first ordered 4-tuple to
the second. We work out the analogous statement for unordered
sets of 4 distinct points.
Let j be the rational function (of degree 6)
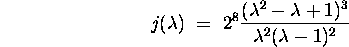
The composition 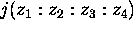 , of j and the cross ratio,
is called the j-invariant of the unordered set
, of j and the cross ratio,
is called the j-invariant of the unordered set 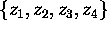 .
Use your answer to problem 11 to show
.
Use your answer to problem 11 to show
-
The function
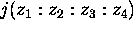 is symmetric in the
is symmetric in the 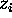 .
. -
There exists a linear fractional transformation mapping the unordered set
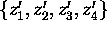 onto
onto 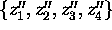 if and only if
their j-invariants are equal.
if and only if
their j-invariants are equal.
-
Lang Ch III Sec 2 page 102 problems 5, 7
-
-
Describe the curve C parametrized by
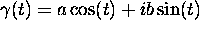 ,
, 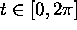 .
Compute
.
Compute
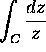 .
. -
Compute
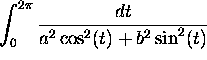 .
.
-
-
Let
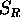 denote the semi-circle
denote the semi-circle
Show that 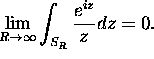
-
Let
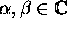 be such that
be such that 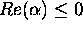 and
and
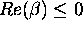 . Show that
. Show that
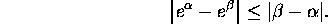
The following three challenge problems are a continuation of
problem 12. They will be due only if and when we study
elliptic functions. You have the knowledge required to answer the questions, so
if you can afford the time, enjoy solving them.
-
Given a complex number
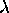 , we define
the elliptic curve
, we define
the elliptic curve 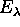 to be the cubic ``curve'' in
to be the cubic ``curve'' in
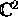 given by the equation
given by the equation

Let f be a l.f.t mapping the set 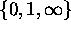 to itself (see
problem 11). Show that
there is a constant c, depending of f and
to itself (see
problem 11). Show that
there is a constant c, depending of f and 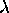 uniquely up to sign,
for which the map
uniquely up to sign,
for which the map
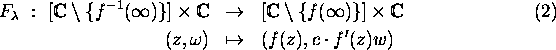
is invertible and it
maps the corresponding open set of 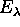 onto that of
onto that of
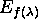 . (Show it for two l.f.t generating
. (Show it for two l.f.t generating 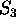 and explain
why it follows for all six).
and explain
why it follows for all six).
Note:
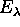 is a surface in
is a surface in 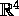 . A basic result in the theory of
elliptic functions shows
. A basic result in the theory of
elliptic functions shows 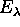 to be homeomorphic to
the surface of a donut with one point removed
(Theorem 2.3 page 399 in Lang).
The complete elliptic curve
to be homeomorphic to
the surface of a donut with one point removed
(Theorem 2.3 page 399 in Lang).
The complete elliptic curve 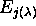 is defined
in a way analogous to the extended complex plane. Simply,
regard
is defined
in a way analogous to the extended complex plane. Simply,
regard 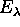 and
and 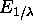 as two open sets
of
as two open sets
of 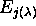 and identify
and identify
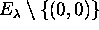 with
with 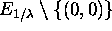 via
(2) (with f(z)=1/z). Problems
11, 12 and
1 imply that
the complete elliptic curve depends only on the j-invariant of
via
(2) (with f(z)=1/z). Problems
11, 12 and
1 imply that
the complete elliptic curve depends only on the j-invariant of
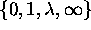 .
.
-
Next, define the notion of an (oriented) angle between two intersecting
arcs on
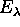 as follows.
as follows.
-
Let
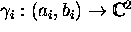 , i=1,2,
be two differentiable maps lying on
, i=1,2,
be two differentiable maps lying on 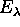 and suppose that
they intersect at the point p,
and suppose that
they intersect at the point p, 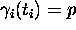 .
Show that their tangent vectors
.
Show that their tangent vectors 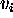 at p
are linearly dependent as complex vectors
in
at p
are linearly dependent as complex vectors
in 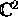 .
. -
If
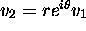 and
and 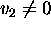 , we define the
oriented angle from
, we define the
oriented angle from 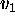 to
to 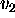 to be
to be 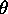 .
.
Show that (2) is a bijective conformal map with respect to
the above definition of angles. Show also that the map
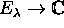 given by
given by 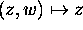 is conformal
away from
is conformal
away from 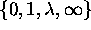 .
.
Note:
Two elliptic curves
with distinct j-invariants can not be related by a bijective
(orientation preserving) conformal map.
-
-
Show that the set of invertible orientation preserving conformal automorphisms
of an elliptic curve
is a group and the subset fixing a point (say at infinity)
is a subgroup.
-
Let G be the group of orientation preserving conformal automorphisms of
an elliptic curve
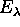 fixing the point
fixing the point 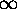 . Show that
G has at least two elements. If
. Show that
G has at least two elements. If 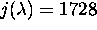 , G has at least 4
elements. If
, G has at least 4
elements. If 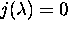 , G has at least 6 elements.
Hint: See problem 11.
, G has at least 6 elements.
Hint: See problem 11.
Note: It can be shown that the number of elements in G is precisely
the one indicated in Part 3b.



Next: About this document
Eyal Markman
Fri Feb 25 12:47:19 EST 2000
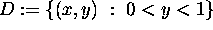 and such that
and such that 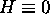 on the line
on the line 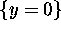 and
and 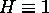 on the line y=1.
on the line y=1.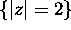 and outside the circle
and outside the circle 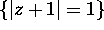 and such that
and such that
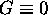 on the inner circle and
on the inner circle and 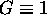 on the outer circle.
Hint: See HW 2 problem 2(a).
on the outer circle.
Hint: See HW 2 problem 2(a).
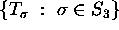 .
.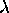 is the set
is the set
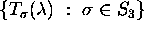 .
Show that all but two
.
Show that all but two  orbits in
orbits in
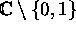 consist of six elements.
One special
consist of six elements.
One special 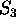 orbit in
orbit in
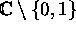 consists of two elements and
the other special orbit consists of three elements.
consists of two elements and
the other special orbit consists of three elements.
![]()
![]() , of j and the cross ratio,
is called the j-invariant of the unordered set
, of j and the cross ratio,
is called the j-invariant of the unordered set ![]() .
Use your answer to problem 11 to show
.
Use your answer to problem 11 to show
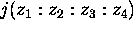 is symmetric in the
is symmetric in the 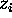 .
.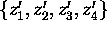 onto
onto 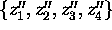 if and only if
their j-invariants are equal.
if and only if
their j-invariants are equal.
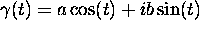 ,
, 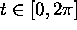 .
Compute
.
Compute
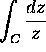 .
.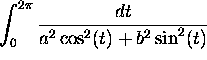 .
.
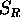 denote the semi-circle
denote the semi-circle
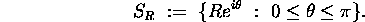
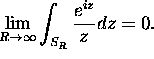
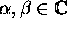 be such that
be such that 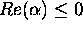 and
and
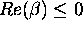 . Show that
. Show that