a)
Find the principal part at ![]() of the function
of the function
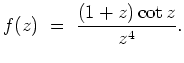
Answer:
![]() The part shown is the principal part.
The part shown is the principal part.
b) Find all the singularities of ![]() in the disk
in the disk
![]() .
Determine the nature of each singularity (isolated, removable,
pole of what order, essential).
.
Determine the nature of each singularity (isolated, removable,
pole of what order, essential).
Answer:
Zero is a pole of order ![]() . The function
. The function ![]() can be written in the form
can be written in the form
![]() , where
, where
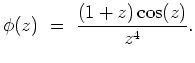 Integral multiples of
Integral multiples of ![]() are simple zeroes
(of order
are simple zeroes
(of order ![]() )
of the function
)
of the function ![]() , of which
, of which ![]() ,
, ![]() , and
, and ![]() are in the disk
are in the disk ![]() . The function
. The function ![]() does not vanish at
does not vanish at ![]() and
and ![]() . Hence,
. Hence, ![]() and
and ![]() are simple poles of
are simple poles of ![]() .
.
c)
Find the residue at each isolated singularity in ![]() .
.
Answer:
Using the Laurent serries above, we see that
![]() .
At the simple pole
.
At the simple pole ![]() , the residues is
, the residues is
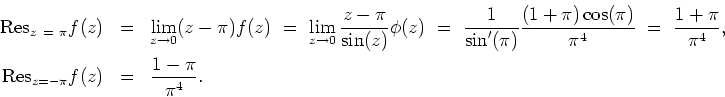
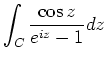 ,
where
,
where
Answer:
![]() vanishes to order
vanishes to order ![]() at integer multiples of
at integer multiples of ![]() (because
(because
![]() ).
The numerator
).
The numerator ![]() has value
has value ![]() at
at ![]() . Thus,
. Thus,
![]() has a simple pole at
has a simple pole at ![]() ,
, ![]() .
The only multiple of
.
The only multiple of ![]() enclosed by
enclosed by ![]() is
is ![]() .
Using the fact that
.
Using the fact that ![]() is a simple pole, we get
is a simple pole, we get
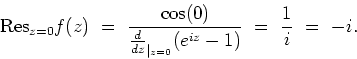
Cauchy's Theorem yields,
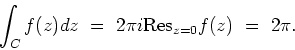
Answer:
![]() is an entire function, so its integral, over any closed
contour, is zero (by Cauchy-Goursat's Theorem).
Using the parametrization
is an entire function, so its integral, over any closed
contour, is zero (by Cauchy-Goursat's Theorem).
Using the parametrization
![]() , we get
, we get
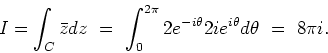
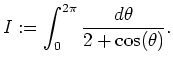
Answer:
Let ![]() . Then
. Then
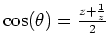 ,
,
![]() and
and
![]() .
The integral gets converted to the contour integral over the unit circle
.
The integral gets converted to the contour integral over the unit circle ![]() .
.
![\begin{displaymath}
I=\int_C\frac{1}{2+\left[\frac{z+\frac{1}{z}}{2}\right]}\frac{dz}{iz}
\ = \
(-2i)\int_C\frac{dz}{z^2+4z+1}.
\end{displaymath}](img41.gif)
The integrand has poles at
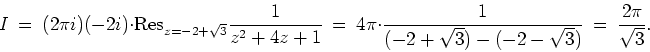
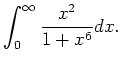
Answer: See the first Example in Section 60 of the text on page 205.
Answer:
Let
![]() be the Taylor series of
be the Taylor series of ![]() centered at
centered at ![]() . Taylor's Theorem states, in particular, that
. Taylor's Theorem states, in particular, that
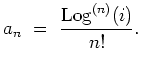 Now,
Now,
![]() and
and
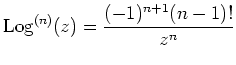 for
for ![]() . We get, for
. We get, for ![]() ,
,
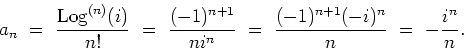
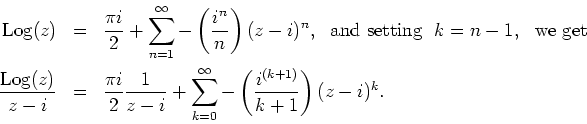
b)
Find the Taylor series of the function
![]() around the point
around the point ![]() .
.
Answer:
Use the partial fraction decomposition
Now, use the Taylor series of
![\begin{eqnarray*}
\frac{-1}{z-1} & = & \frac{1}{1-z} \ = \
\sum_{n=0}^\infty z^...
...m_{n=0}^\infty \left[1-\left(\frac{1}{2}\right)^{n+1}\right]z^n.
\end{eqnarray*}](img63.gif)
a) The limit
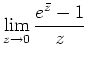 exists and is equal to
exists and is equal to ![]() .
.
Answer:
False, ![]() is not analytic at
is not analytic at ![]() . The above limit is the derivative
limit, which does not exists. A direct argument, that the limit doesn't
exists, consists of letting
. The above limit is the derivative
limit, which does not exists. A direct argument, that the limit doesn't
exists, consists of letting ![]() approach
approach ![]() along the
along the ![]() and
and ![]() axis:
axis:
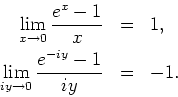
b)
There is a function ![]() , analytic in the disk
, analytic in the disk
![]() ,
such that
,
such that
Answer:
False. Such a function ![]() would be a non-constant
analytic function, whose absolute value achieves its
maximum at the interior point
would be a non-constant
analytic function, whose absolute value achieves its
maximum at the interior point ![]() of
of ![]() . This contradicts the
Maximum Modulus Principle.
. This contradicts the
Maximum Modulus Principle.
c)
If ![]() has an isolated singularity at
has an isolated singularity at ![]() and
and
![]() , then
, then
![]() is a removeable singularity.
is a removeable singularity.
Answer:
False. Take
![]() and
and ![]() as a counter example.
as a counter example.
Answer:
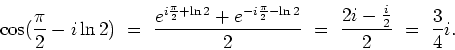
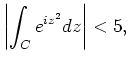 where
where
Answer:
The curve ![]() is parametrized by
is parametrized by
![]() ,
,
![]() .
Thus,
.
Thus,
![]() has a positive imaginary part. Consequently,
has a positive imaginary part. Consequently,
![]() has a negative real part equal to
has a negative real part equal to
![]() , where
, where
![]() , and
, and
We conclude, that
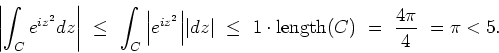
Answer:
Note the equality
Take