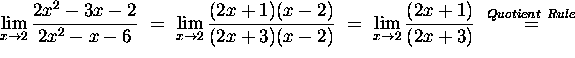
Math 131 Exam 1 Solution Fall 1999
1. (25 points)
a)
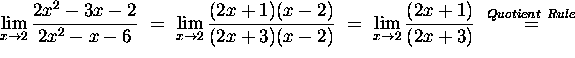
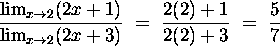
b) Support your result in part (a) both by a table and by a graph
of the function 
in a window
containing the point 
. Notice that
.
2.
a) The function
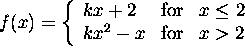is continuous at the point x=2 if and only if
the two one sided limits
and
are equal.
We determine the value of k for which the function is continuous by
i) calculating each of the one sided limits in terms of k.
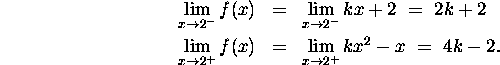
ii) set them equal to each other
and solve for k to get k=2.
b)
The function is not differentiable even when k=2 because we have
a corner at the point (2,6) on the graph.
This can be seen by comparing the derivatives at the point x=2 of
the two functions 2x+2 and 
(which are not equal). More precisely,
we calculate the left hand and right hand derivative limits:
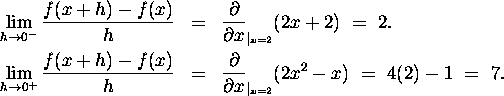
Since they are not equal, the derivative limit does not exist.
3. a) A line x=a is a vertical asymptotes of the function
if and only if a one sided limit is infinite
The candidates for vertical asymptotes are the roots x=1 and x=-4 of the denominator. We need, however, to check that a one sided limit is indeed infinite (In question 1, for example, 2 is a root of the denominator, but x=2 is not a vertical asymptote).
In our case, x=1 is a vertical asymptote because the numerator does not vanish at x=1. (If you stopped here you got the full credit). Similarly, x=-4 is a vertical asymptote because the numerator does not vanish at x=-4. We can show the vertical asymptotes by a graph: A precise answer would include a calculation of the one sided limits algebraically:
Similarly,
b)
The line y=k is a horizontal asymptote of the function
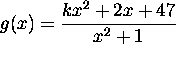because
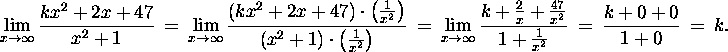
Thus, for the line y=3 to be a horizontal asymptote, we choose k=3.
4.
We calculate the derivative of 
using the definition of the derivative as
follows:
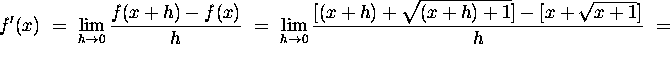
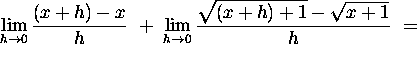
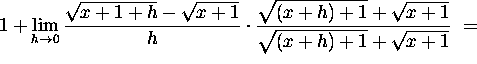
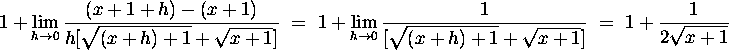
5. Let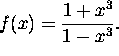 
Using the derivative formula for a quotient,
we compute:
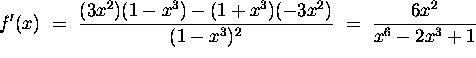
6.
a) The derivative of
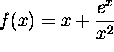is
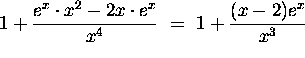
b) The equation of the tangent line through the point (1,1+e) is
Using part a) we get that 
.
So, the tangent line is
7.
a) Using the product rule we see that, if 
, then
b) If g'(0)=5, then
so f(0)=5.