by an algebraic procedure. Show all your algebraic steps.
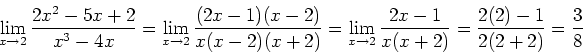
b) (5) Support your result in part a) with a calculator. Describe your procedure and show as much data as possible.
| x | y |
| 1.9 | .377868 |
| 1.99 | .375310 |
| 1.9999 | .375003 |
| 1.999999 | .375000 |
| 2.1 | .371661 |
| 2.01 | .374685 |
| 2.0001 | .374997 |
| 2.000001 | .374999 |
As the values of ![]() approach 2 either from the right or from the
left (but not equal to 2) the values of
approach 2 either from the right or from the
left (but not equal to 2) the values of ![]() approach
approach ![]() .
.

where
a) (5)
Find
![]() and
and
![]() .
.
b) (5)
What conditions do ![]() and
and ![]() have to satisfy, so that
have to satisfy, so that ![]() is
continuous at
is
continuous at ![]() .
.
For ![]() to be continuous at
to be continuous at ![]() we need the limit
we need the limit
![]() exist and equal
exist and equal
![]() . Since
. Since ![]() and
and
![]() exists if and only if
exists if and only if
![]() we see
that the condition on
we see
that the condition on ![]() and
and ![]() is
is ![]() .
.
c) (5)
Find ![]() and
and ![]() , such that
, such that ![]() is everywhere differentiable.
is everywhere differentiable.
First ![]() must be continuous everywhere, thus
must be continuous everywhere, thus ![]() from part
b). Notice that
from part
b). Notice that ![]() is differentiable at each
is differentiable at each ![]() . The
derivative at
. The
derivative at ![]() is the limit
is the limit
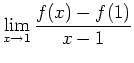 . It exists if and
only if the left hand and the right hand derivative limits are
equal. We have
. It exists if and
only if the left hand and the right hand derivative limits are
equal. We have
Therefore
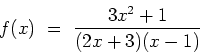
Explain your reasons.
The vertical asymptotes are the lines ![]() such that the
denominator is zero at
such that the
denominator is zero at ![]() , but the numerator is not. We have
, but the numerator is not. We have
![]() , i.e.
, i.e. ![]() or
or ![]() . Since
. Since
![]() and
and
![]() the vertical
asymptotes are
the vertical
asymptotes are ![]() and
and ![]() .
.
The horizontal asymptotes are the lines ![]() where
where ![]() is the
limit of
is the
limit of ![]() as
as ![]() approaches positive or negative infinity.
We have
approaches positive or negative infinity.
We have

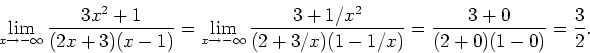
Therefore the only horizontal asymptote is ![]() .
.
b) (5) Graph the function in part a) indicating all horizontal and vertical asymptotes.
One can first write
![]() . Then
. Then
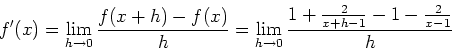
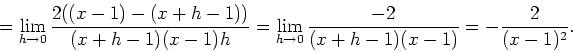
Another way is

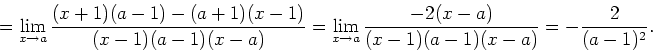
a) (5) Find the velocity of the ball after
The velocity function is the derivative of the height function
with respect to the time ![]() . Thus
. Thus
![]() .
.
b) (5) It is observed, that the ball hits the ground with
a speed of ![]() feet per second. How long was the ball in the air?
Hint: The speed is the absolute value of the velocity.
feet per second. How long was the ball in the air?
Hint: The speed is the absolute value of the velocity.
At the moment when the ball hits the ground the velocity is ![]() ft/s (the velocity vector points downward). We get
ft/s (the velocity vector points downward). We get ![]() ,
i.e.
,
i.e. ![]() , which means that the ball was 4 seconds in the air.
, which means that the ball was 4 seconds in the air.
c) (5) Use the information in part b) to determine the height of the tower.
When the ball hits the ground the height of the ball is zero. On
the other hand, it is the height of the ball after 4 seconds, thus
we get ![]() , i.e.
, i.e. ![]() and
and ![]() .
.
Find an equation for the tangent line to the graph of
The slope of the tangent line to the graph of ![]() at the point
at the point ![]() is equal to the derivative of
is equal to the derivative of ![]() at
at ![]() . By definition the derivative
of
. By definition the derivative
of ![]() at
at ![]() is the limit
is the limit
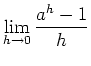 .
We are given that this limit is equal to 17, so the slope of the tangent
is 17. Since the tangent passes through the
point
.
We are given that this limit is equal to 17, so the slope of the tangent
is 17. Since the tangent passes through the
point ![]() the equation of the tangent is
the equation of the tangent is ![]() , i.e.
, i.e. ![]() .
.
b) (7) Find a formula for the derivative ![]() of the following function
of the following function

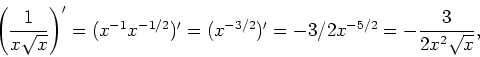
Therefore,
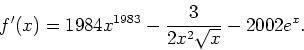
By the quotient rule
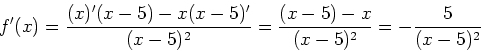
b) (5)
Find the equation of the tangent line to the graph of ![]() at the point
at the point ![]() .
.
The slope of the tangent line to the graph of ![]() at
at ![]() is
is ![]() . By part a)
. By part a)

Since the line passes through