1) (4 points) A rectangular box with a square base and a volume of
675 cubic centimeters is to be constructed.
The sides cost $1.25 per square centimeter and
the top and bottom cost $2.00 per square centimeter.
If the dimensions of the box are
![]() cm
then the cost function C(x,h) is:
cm
then the cost function C(x,h) is:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(e) ![]()
(f) none of the above
Answer: (c)
![]() .
.
2) (6 points) Find the dimensions which minimize the cost.
(a) 2.5 cm ![]() 2.5 cm
2.5 cm ![]() 108 cm
108 cm
(b) 4.5 cm ![]() 4.5 cm
4.5 cm ![]() 33.3 cm
33.3 cm
(c) 6.5 cm ![]() 6.5 cm
6.5 cm ![]() 16 cm
16 cm
(d) 7.5 cm ![]() 7.5 cm
7.5 cm ![]() 12 cm
12 cm
(e) 8 cm ![]() 8 cm
8 cm ![]() 10.25 cm
10.25 cm
(f) 10 cm ![]() 10 cm
10 cm ![]() 6.75 cm
6.75 cm
(g) none of the above
Answer: (d)
Step 1: The constraint equation is
![]()
Step 2:
Use the constraint equation in order to
express the cost function as a function of one
veriable (say x). Since ![]() , we get that the cost,
as a function of x, is
, we get that the cost,
as a function of x, is
![]()
Step 3: Minimize the cost by solving
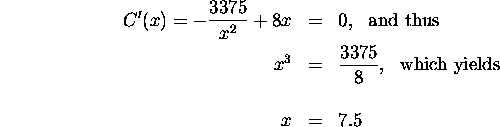
We can verify that x=7.5 is the absolute minimum by using the first
derivative test: C'(x) is negative in the interval
![]() and positive in the interval
and positive in the interval ![]() .
.