and 
on this interval. Which of the
following grapfs best
illustrates this function?
Math 127 Section 5 QUIZ 5
Name: (PRINT!!!)
Student ID:
1) (5 points) Suppose f is a function defined on the interval (a,b) and
and on this interval. Which of the
following grapfs best
illustrates this function?
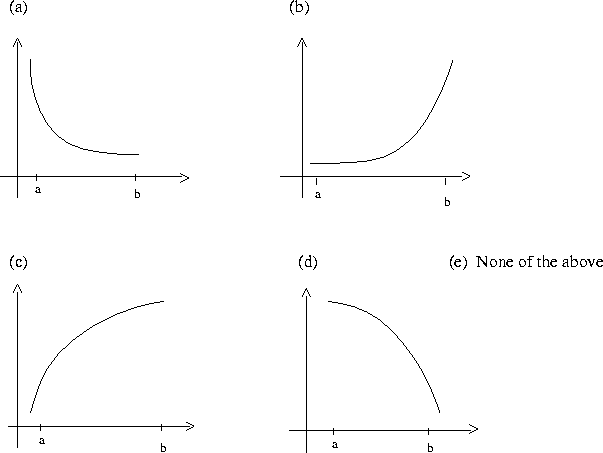
Answer: (c)
2) (5 points) Let f(x) be a differentiable function. If the graph of its derivative f'(x) is given below
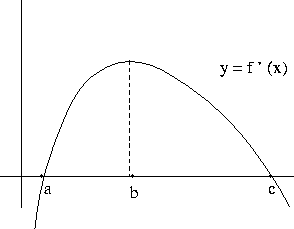
i) the point (a,f(a)) on the graph y = f(x) of the original function
is
(a) a relative maximum,
(b) a relative minumum,
(c) an inflection point.
Answer: (b) The point (a,f(a)) is a relative minimum because f'(x)
is negative (so the function f(x) is decreasing)
in the interval 
and f'(x) is positive
(so the function f(x) is increasing) in the interval
.
ii) the point (b,f(b)) on the graph y = f(x) of the original
function is
(a) a relative maximum,
(b) a relative minumum,
(c) an inflection point.
Answer: (c)
The slope f'(x) is increasing on the interval
(so the function f(x) in concave up on this interval)
and the slope f'(x) is decreasing on the interval
(so the function f(x) in concave down on this interval). Hence,
the point (b,f(b)) is an inflection point.
iii) the point (c,f(c)) on the graph y = f(x) of the original
function is
(a) a relative maximum,
(b) a relative minumum,
(c) an inflection point.
Answer: (a) The point (c,f(c)) is a relative maximum. The reasoning is similar to part i).
| Old grade | New grade |
| 10 | 10 |
| 9 | 10 |
| 8 | 8 |
| 7 | 10 |
| 5 | 8 |
| 4 | 4 |
| 3 | 3 |
| 2 | 3 |
| 0 | 3 |