Let f be a holomorphic function defined and having a continuous derivative f' in an open set U containing a rectangle R. Then
![]()
Recall the statement of Green's Theorem: Let ![]() be an oriented
piecewise smooth simple path (i.e., each connected component of
be an oriented
piecewise smooth simple path (i.e., each connected component of
![]() does not intersect itself)
in the plane. Assume that
does not intersect itself)
in the plane. Assume that ![]() bounds a region D
(and has the induced orientation, i.e., each smooth piece of
bounds a region D
(and has the induced orientation, i.e., each smooth piece of ![]() is oriented so that D is on the left as you move along
is oriented so that D is on the left as you move along ![]() ).
Let p(x,y), q(x,y) be two functions which are defined and have
continuous partial derivatives in an open set
).
Let p(x,y), q(x,y) be two functions which are defined and have
continuous partial derivatives in an open set ![]() containing D and
containing D and ![]() . Then
. Then
![]()
-
Let D be an open disk in
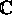 and let f be continuous in D.
Suppose that
and let f be continuous in D.
Suppose that 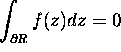 for every closed rectangle R contained in D. Prove that f is
holomorphic.
for every closed rectangle R contained in D. Prove that f is
holomorphic. -
Suppose that f is continuous in all of
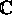 and holomorphic in
and holomorphic in 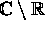 .
Prove that f is holomorphic everywhere.
.
Prove that f is holomorphic everywhere.
(a)
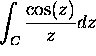 (b)
(b)
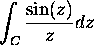 (c)
(c)
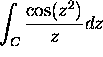
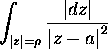 under the condition
under the condition -
Let f be an entire function, k a positive integer,
and let
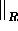 be the maximum of
be the maximum of
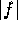 on the circle of radius R centered at the origin.
Then f is a polynomial of degree
on the circle of radius R centered at the origin.
Then f is a polynomial of degree 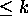 if and only if
there exist constants C and
if and only if
there exist constants C and 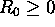 such that
such that

for all
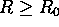 . (Note: one direction was proven in HW 1 Problem 7).
. (Note: one direction was proven in HW 1 Problem 7). -
Ahlfors, page 130 Problem 2: Show that a function which is analytic in the
whole plane and has a non-essential singularity at
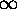 reduces to a
polynomial.
reduces to a
polynomial.
![]()
Hint: Use polar coordinates and Cauchy's Formula.
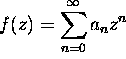 be
the Taylor series expansion of f. Show that
be
the Taylor series expansion of f. Show that
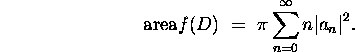
-
Show that the functions
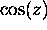 and
and 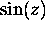 have essential singularities
at
have essential singularities
at 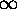 .
. -
Let
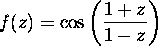 ,
, 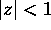 .
Find the set
.
Find the set 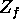 of zeroes of f. Does
of zeroes of f. Does 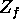 have any accumulation points?
Explain. (See Lang, page 21 for the definition of an
accumulation point).
have any accumulation points?
Explain. (See Lang, page 21 for the definition of an
accumulation point).