![]()
Show that the real and imaginary parts of f satisfy the Cauchy-Riemann equations at z=0. Is f holomorphic at z=0?
-
Let
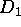 and
and 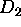 be open connected sets in
be open connected sets in 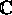 and
and
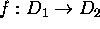 a holomorphic map. Show that if H is harmonic
in
a holomorphic map. Show that if H is harmonic
in 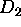 , then
the composition
, then
the composition 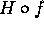 is harmonic in
is harmonic in 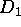 .
. -
Let
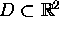 be a connected open set and
u(x,y), v(x,y) harmonic in D. Prove or disprove the following
statements:
be a connected open set and
u(x,y), v(x,y) harmonic in D. Prove or disprove the following
statements:
-
The function
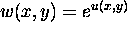 is harmonic in D.
is harmonic in D. - The function w(x,y) = u(x,y)v(x,y) is harmonic in D.
-
If v is a harmonic conjugate of u, the function
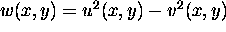 is harmonic in D.
is harmonic in D.
-
The function
-
Prove that the functions f(z) and
 are simultanously
holomorphic (this is a special case of the Reflection Principle).
are simultanously
holomorphic (this is a special case of the Reflection Principle). -
Following Lang, we will say that a function f is analytic
in an open set
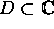 , if for every point
, if for every point 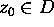 ,
f has a power series expansion centered at
,
f has a power series expansion centered at 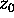
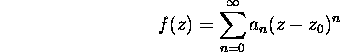
with a positive radius of convergence. (We will see later that a function is analytic if and only if it is holomorphic, but do not assume it now). Prove that the functions f(z) is analytic in D if and only if
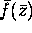 is analytic in
is analytic in 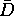 .
.
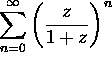 convergent? (Describe the set geometrically).
convergent? (Describe the set geometrically). ![]()
-
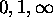 to 1, -1, 0,
to 1, -1, 0, - 0, i, -i to 1, -1, 0.
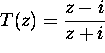 .
Determine the image of horizontal lines Im(z)=b under T.
When the image is a circle, determine the center and radius.
.
Determine the image of horizontal lines Im(z)=b under T.
When the image is a circle, determine the center and radius.