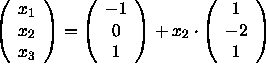, whichever is higher.
In other words, if your score on question 2 is low, your grade was calculated as if question 2 was worth 20% instead off 35%
(and the rest 80% instead off 65%).
Math 235 Solution for Midterm 1 Spring 1999
Your grade was calcultated as follows: If your score on question 2 is x and your total score is y then your grade is either y or
, whichever is higher.
In other words, if your score on question 2 is low, your grade was calculated as if question 2 was worth 20% instead off 35%
(and the rest 80% instead off 65%).
is obtained as follows:
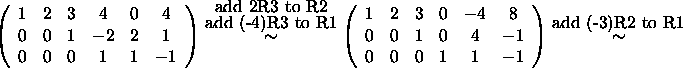
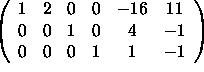
Note: The row reduction takes only 3 elementary row operations. If you needed more than three then you need to review the row reduction algorithm!
b) Two variables, 
, 
are free variables.
The general solution of the system is
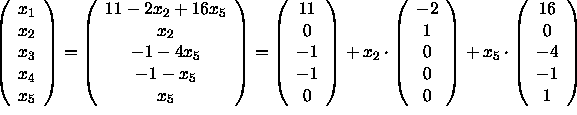
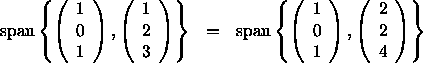
The statement is True. The two planes in 
are equal!
Reason:
Denote by 
the two vectors on the left hand side, and by
the two vectors on the right hand side. Then
If you mentioned relation (1) as a reason, you got the full credit. The complete argument proceeds as follows:
If u is a vector in 
, then it is a linear
combination 
. Using the relations (1)
we can express u as a linear combination of 
and 
:
Hence, u is in 
.
Conversely, If u is a vector in ,
then it is a linear combination 
.
Using the relations (1)
we can express u as a linear combination of 
and 
:
Hence, u is in .
matrix are linearly dependent.
The statement is True. There are more columns than entries in each column.
is linearly dependent, then the set contains
more than n vectors.
The statement is False.
Counter Example:
The set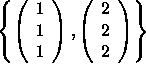 
in in linearly dependent but contains only 2 vectors.
has a unique solution, then the columns of
the matrix A are linearly independent.
The statement is True.
Note: If you said that it is a theorem in the text, or proven in class,
you got the full credit. The full explanation is:
Solutions 
of the system are coefficients of linear combinations of columns of A
which are equal to zero. If there is a unique solution,
then the trivial solution must be
this unique solution. Hence, if a linear combination
of the columns of A
is equal to 
, then all coefficients 
are 0.
This is the definition of linear independence.
matrix A are linearly independent,
then the system 
is consistent for every vector 
in .
The statement is False.
Counter Example: Take
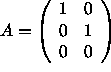and
.
matrices and C=AB their product.
If the third column 
of B is a linear combination of the first two columns
, 
, then the third column 
of C is a linear combination of the first two columns
, 
.
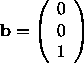The statement is True.
Reason: Use the definition of matrix multiplication.
If 
then
So is a linear combination of and .
is a linearly dependent set in 
, then
the vector 
is a linear combination of and .
The statement is False.
Counter Example:
in the following circuit using i) the junction rule:
the sum of currents entering a junction is equal to the sum
of currents leaving the junction.
ii) Ohm's rule: The drop in the voltage 
across a resistance
R is related to the (directed) current I by the equation
.
iii) Kirchhof's circuit rule: the sum of the voltage drops due to resistances
around any closed loop in the circuit equals the sum of the voltages induced
by sources along the loop.
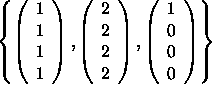
All resistances below are equal to 
.
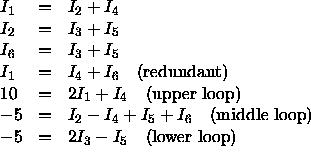
Note: If you used loop currents 
, 
, 
instead of
branch currents then you got the full credit if you wrote:
a) T is the map from 
to defined by
.
Not a linear transformation. (Because of the quadratic term
). It violates the property
. Take for example c=2 and 
.
Then T(2(1,1))=T(2,2)=(10,4) which is different from
2T(1,1)=2(5,1)=(10,2).
It violates also the additivity the property
. Check!
b) T is the map from to defined by
.
Linear transformation. Its standard matrix is
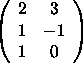
c) T is the map from to which is the
composition of the rotation of the plane 90
degrees counterclockwise, followed by reflection
with respect to the -axis.
Linear transformation. Its standard matrix is
answer
both questions: ? and
ii) Is it linearly independent? Justify your answer!!!
(No credit will be given for an answer without a justification).
,
,
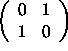
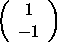The matrix
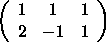is row equivalent to
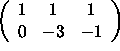which is in echelon form.
(i) Yes, the set spans because the matrix
has a pivot in every row.
(ii) No, the set is linearly dependent because not every column is a pivot column. (There are more columns than rows).
,
The matrix
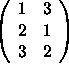is row equivalent to
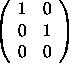
(i) No, the set does not span because
there does not exist a pivot in every row (there are less vectors than
entries in each vector).
(ii) Yes, the set is linearly independent because there is a pivot in every column.
,
,
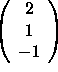The matrix
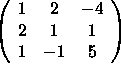is row equivalent to
.
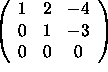(i) No, the set does not span because there does not
exist a pivot in every row.
(ii) No, the set is linearly dependent because there does not exist a pivot in every column.
(10 points) Let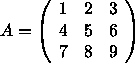 
,
,
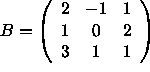and C=AB their product.
a) Compute the (3,2) entry of C.
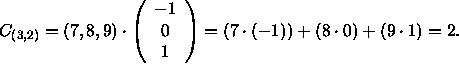
b) Let be the second column of C.
Solve (with as little computations as possible)
the system of linear equations 
.
Since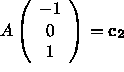 
,
then 
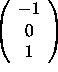is a particular solution.
If you stopped here you still got the full credit.
The row reduced echelon form of the matrix A is
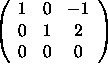The general solution is
