Math 235 Midterm 1 Spring 1999

1. a) Find the row reduced echelon augmented matrix of the system
   
   
   

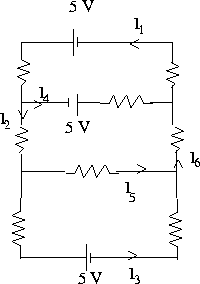
   b) Find the general solution for the system.

2. Determine if the statements are true or false. If it is true, give a reason. If it is false, provide a counter example:
   1. 
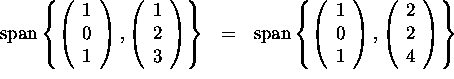
   2. The columns of any 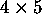matrix are linearly dependent.
   3. If a set in 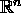is linearly dependent, then the set contains more than n vectors.
   4. If the system 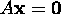has a unique solution, then the columns of the matrix A are linearly independent.
   5. If the columns of a 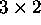matrix A are linearly independent, then the system 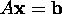is consistent for every vector 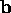in .
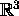   6. Let A and B be two 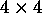matrices and C=AB their product. If the third column 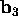of B is a linear combination of the first two columns 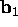, , 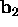then the third column 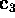of C is a linear combination of the first two columns , .
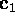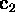   7. If 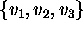is a linearly dependent set in 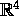, then the vector 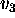is a linear combination of 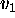and .

3.   Set up a system of linear equations for finding the electrical currents in the following circuit using i) the junction rule: the sum of currents entering a junction is equal to the sum of currents leaving the junction. ii) Ohm's rule: The drop in the voltage across a resistance R is related to the (directed) current I by the equation . iii) Kirchhof's circuit rule: the sum of the voltage drops due to resistances around any closed loop in the circuit equals the sum of the voltages induced by sources along the loop.

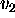   All resistances below are equal to . Note: Do not solve the system.

   

4. For each of the following maps, determine if it is a linear transformation. If it is, find its standard matrix. If it is not, explain which property of linear transformations it violates (and why it violates it).

   a) T is the map from to defined by .

   b) T is the map from to defined by .

   c) T is the map from to which is the composition of the rotation of the plane 90 degrees counterclockwise, followed by reflection with respect to the -axis.

5. For each of the following sets of vectors in answer both questions:
   i) Does the set span the whole of ? and ii) Is it linearly independent? Justify your answer!!! (No credit will be given for an answer without a justification).
   1. , ,
   2. ,
   3. , ,

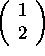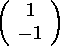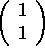
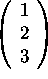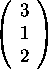
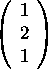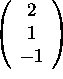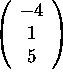
6. Let 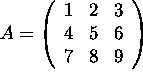, , 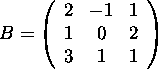and C=AB their product.

   a) Compute the (3,2) entry of C.

   b) Let be the second column of C. Solve (with as little computations as possible) the system of linear equations .

• About this document ...