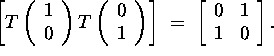Answer: The row reduction takes four steps:
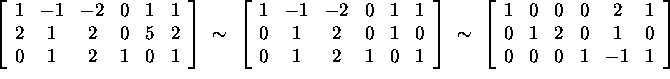
b) Find the general solution for the system.
Answer:
![]() and
and ![]() are free variables.
are free variables.
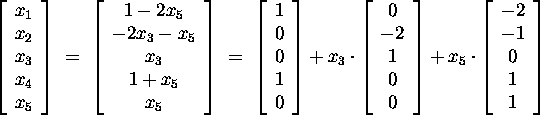
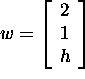 be in the plane passing through
be in the plane passing through
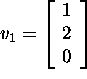 ,
,
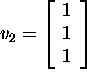 , and the origin (zero vector).
, and the origin (zero vector).
Answer: The question is equivalent to:
``For which value of h is w in the plane spanned by ![]() and
and ![]() ?''
?''
The latter question is equivalent to:
``For which h is the system, corresponding to the following augmented matrix, consistent?''
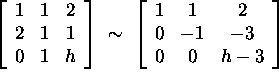
If h=3, the system is consistent, and w is a linear combination of ![]() and
and ![]() (indeed,
(indeed, ![]() ).
).
If ![]() , the system is inconsistent and w does not belong to
, the system is inconsistent and w does not belong to
![]() .
.
b) (8 points)
Find two vectors ![]() ,
, ![]() which span the plane P given by the equation
which span the plane P given by the equation
![]()
(i.e., such that ![]() ).
).
Answer:
Once we write the solution of the system (of one equation)
in parametric form, we exhibit the solution set (i.e., the plane P)
as a ``span''. The variables ![]() and
and ![]() are free. We get
are free. We get
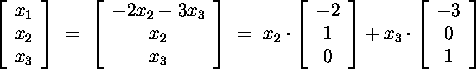
The two vectors on the right span the plane P.
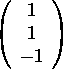
i) (5 points) linearly independent?
Answer:
Yes, the two vectors are linearly independent. A row echelon matrix is
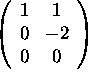 .
It has a pivot in every column.
.
It has a pivot in every column.
ii) (5 points) Does it span ![]() ? Justify you answers!
? Justify you answers!
Answer: No, the two vectors do not span ![]() . We
do not have a pivot in every row. (There are less vectors than entries in
each vector).
. We
do not have a pivot in every row. (There are less vectors than entries in
each vector).
b) For which values of h will the vectors
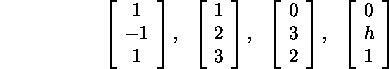
i) (5 points) be linearly independent?
Answer: Never.
Four vectors in ![]() are always linearly dependent.
are always linearly dependent.
ii) (5 points) span ![]() ?
?
Answer: Row reduce.
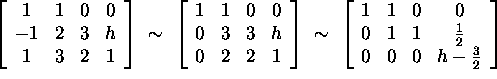
If ![]() , then we have a pivot in every row
(and the four vectors span
, then we have a pivot in every row
(and the four vectors span ![]() ).
).
Note: Do not solve the system.
Answer using branch currents: Using the junction rule we get:
![]()
![]()
![]()
![]()
Using the Voltage loop law, we get:
![]()
![]()
![]()
Answer using loop currents: (The loop currents, denoted ![]() ,
,
![]() ,
, ![]() , correspond to the counterclockwise direction in each loop).
, correspond to the counterclockwise direction in each loop).
![]()
![]()
![]()
A complete answer requires expressing the branch currents in terms of the loop currents: (no credit was deducted if you skipped this part).
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
-
Let
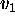 ,
,  ,
, 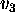 be three vectors in
be three vectors in 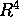 .
Then the set
.
Then the set 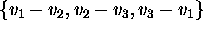 is linearly dependent
(regardless of the choice of
is linearly dependent
(regardless of the choice of 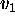 ,
,  ,
, 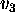 ).
).
Answer: TRUE. Let
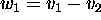 ,
, 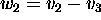 , and
, and 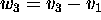 .
The three vectors
.
The three vectors 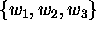 satisfy the linear relation
satisfy the linear relation
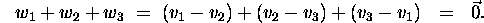
-
The columns of any
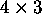 matrix are linearly dependent.
matrix are linearly dependent.
Answer: FALSE. Counter Example:
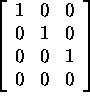
-
If the columns of a
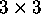 matrix span
matrix span 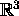 , then
they are linearly independent.
, then
they are linearly independent.
Answer:
TRUE. Since the columns span ![]() , we have a pivot in every
row. Since the matrix is a square matrix, it must also have
a pivot in every column. Consequently, the columns are linearly
independent.
, we have a pivot in every
row. Since the matrix is a square matrix, it must also have
a pivot in every column. Consequently, the columns are linearly
independent.
a) (6 points)
T is the map from ![]() to
to ![]() defined by
defined by
![]() .
.
Answer: A linear transformation with standard matrix
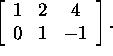
b) (6 points)
T is the map from ![]() to
to ![]() defined by
defined by
![]() .
.
Answer: Not a linear transformation. If it were linear, it would satisfy:
(1) ![]() , for any two vectors in
, for any two vectors in
![]() , and
, and
(2) ![]() , for any scalar c and vecotr
, for any scalar c and vecotr ![]() .
.
It fails to satisfy both (1) and (2). Take for example ![]() and
and ![]() . Then
T((0,0)+(1,1))=T(1,1)=(3,4), while
T(0,0)+T(1,1)=(1,3)+(3,4)=(4,7). So,
. Then
T((0,0)+(1,1))=T(1,1)=(3,4), while
T(0,0)+T(1,1)=(1,3)+(3,4)=(4,7). So,
![]()
and (1) is not satisfied. You can check that (2) fails if you take
![]() and c=2.
and c=2.
c) (6 points)
T is the map from ![]() to
to ![]() which is the
composition of reflection with respect to the
which is the
composition of reflection with respect to the ![]() -axis followed by
the rotation of the plane 90
degrees counterclockwise.
-axis followed by
the rotation of the plane 90
degrees counterclockwise.
Answer: A linear transformation.
The reflection has the standard matrix
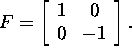 The rotation has the standard matrix
The rotation has the standard matrix
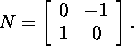
Hence,
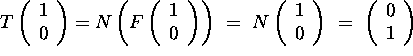 , while
, while
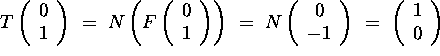
The standard matrix is