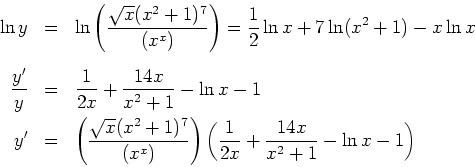Solution:
Differentiating with respect to ![]() we have
we have
Solving for
![]() , we get
, we get
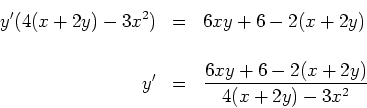
b) (5) Find an equation of the tangent line at the point
Solution: The equation is ![]() , where
, where ![]() is the
value of
is the
value of
![]() when
when ![]() . From (a),
. From (a),
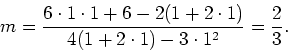
Note: 1 kilometer = 1000 meters.
Solution: Let ![]() be the distance from the car to the
helicopter, and let
be the distance from the car to the
helicopter, and let ![]() be the distance from the car to the point
of the road directly below the helicopter. The problem states that
be the distance from the car to the point
of the road directly below the helicopter. The problem states that
![]() , and asks us to find the value of
, and asks us to find the value of
![]() at the moment when
at the moment when
![]() . By the
Pythagorean Theorem
. By the
Pythagorean Theorem
![]() at any time. Differentiating
at any time. Differentiating
![]() and
and ![]() with respect to time, we get
with respect to time, we get
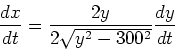
so that
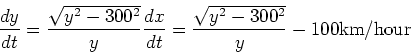
Thus, when
Solution:
![]()
b)
Use the linearization to approximate ![]() .
.
Solution:
![]()
c) Is your approximation greater than or less than the actual value? Justify your answer.
Solution:
![]() is negative for
is negative for
![]() , so that the graph of
, so that the graph of ![]() is concave down on the
domain of
is concave down on the
domain of ![]() . This implies that the tangent line at the point (36,6) will lie
above the graph of
. This implies that the tangent line at the point (36,6) will lie
above the graph of ![]() for
for ![]() . Since the graph of
. Since the graph of ![]() in (a)
is this tangent line, our approximation,
in (a)
is this tangent line, our approximation, ![]() , will be greater than
, will be greater than
![]() .
.
a) Find the intervals on which ![]() is increasing and those on which it is
decreasing.
is increasing and those on which it is
decreasing.
Solution:
![]() . The zeros of
. The zeros of
![]() are
are ![]() . Since
. Since ![]() is differentiable for all
is differentiable for all ![]() , these
are the only critical points of
, these
are the only critical points of ![]() , so that we only need to test the
sign of the derivative on the intervals
, so that we only need to test the
sign of the derivative on the intervals ![]() ,
, ![]() ,
,
![]() , and
, and ![]() . We have:
. We have:
| decreasing | ||
| increasing | ||
| decreasing | ||
| increasing |
b) Find all the local maxima and local minima of ![]() .
.
Solution: We have critical points ![]() . Using the chart
from (a) we find by the First Derivative Test that
. Using the chart
from (a) we find by the First Derivative Test that ![]() is a
local minimum,
is a
local minimum, ![]() is a local maximum, and
is a local maximum, and ![]() is a
local minimum.
is a
local minimum.
c) Find the values of the global maximum and global minimum of ![]() over the interval
over the interval
![]() .
.
Solution: We evaluate ![]() at the endpoints of the interval:
at the endpoints of the interval:
![]() and
and ![]() . Comparing these two values with the local
minima and maxima we find that
. Comparing these two values with the local
minima and maxima we find that ![]() is the global minimum
and
is the global minimum
and ![]() is the global maximum on this interval.
is the global maximum on this interval.
d) Graph the function over the interval
![]() ,
indicating all the local and global extrema.
,
indicating all the local and global extrema.
for some constant real numbers
a) Express the acceleration ![]() in terms of the time variable
in terms of the time variable ![]() and the constants
and the constants ![]() ,
, ![]() , and
, and ![]() .
.
Solution:
![]()
b) Assume now, that
![]() ,
(so
,
(so ![]() ,
, ![]() and
and ![]() ).
Find the time intervals,
where both the
position
).
Find the time intervals,
where both the
position ![]() and velocity
and velocity ![]() are positive.
are positive.
Solution:
![]() when
when
![]() for any integer
for any integer ![]() .
.
![]() when
when
![]() for any integer
for any integer
![]() . Thus both are positive when
. Thus both are positive when ![]() is in the intersection of these
families of intervals, i.e., when
is in the intersection of these
families of intervals, i.e., when
![]() , or
, or
![]() for any intger
for any intger ![]() .
.
c) Is the particle in part b) speeding up or slowing down, when both its position and velocity are positive? justify your answer.
Solution: When
![]() ,
,
![]() which is clearly negative whenever
which is clearly negative whenever ![]() is positive (they have
opposite signs). So in particular, when
is positive (they have
opposite signs). So in particular, when ![]() and
and ![]() are both
positive,
are both
positive, ![]() will be negative. Thus velocity and acceleration will
have opposite directions so that the particle will be slowing down.
will be negative. Thus velocity and acceleration will
have opposite directions so that the particle will be slowing down.
a) Determine the intervals on which the function is concave upward and those on which it is concave downward.
Solution:
![]() exists for all
exists for all ![]() , so that the only critical points of
, so that the only critical points of ![]() will
be where
will
be where ![]() , i.e., where
, i.e., where ![]() , i.e.,
, i.e., ![]() . Thus we
have to test the sign of the second derivative on the intervals
. Thus we
have to test the sign of the second derivative on the intervals
![]() ,
, ![]() , and
, and ![]() . We have
. We have
| concave down | ||
| concave up | ||
| concave down |
b) Determine all points of inflection, if any. Justify your answer!
Solution: Since ![]() exists for all
exists for all ![]() , our only
candidates for inflection points are where
, our only
candidates for inflection points are where ![]() , i.e.,
, i.e., ![]() . From (a), we know that concavity changes at each of these points
so that both are inflection points.
. From (a), we know that concavity changes at each of these points
so that both are inflection points.
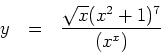
Solution: